1.树的遍历

树的遍历有两种方式：先序遍历和后序遍历。先序遍历是先访问根结点，再依次访问根结点的每棵子树，访问子树时仍然遵循先根再子树的规则；后序遍历是先依次访问根结点的每棵子树，再访问根结点，访问子树时仍然遵循先子树再根的规则。例如，对图6-27所示的树进行先序遍历和后序遍历的过程分别如下：

（1）先序遍历

先访问根结点，然后先序遍历每一棵子树，以图6-27为例：

1）访问根结点A。

2）访问A的第一棵子树，访问子树时先访问根结点B。

3）访问B的第一个孩子E。

4）访问B的第二个孩子F。

5）访问A的第二棵子树，访问子树时先访问根结点C。

6）访问C的第一个孩子G。

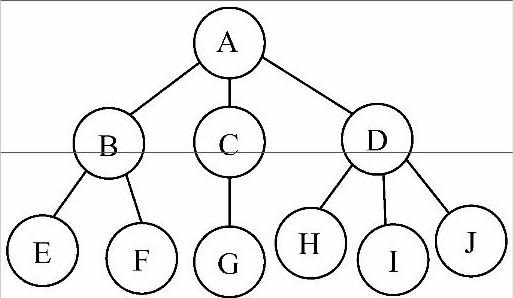
图6-27 树的遍历

7）访问A的第三棵子树，访问子树时先访问根结点D。

8）访问D的第一个孩子H。

9）访问D的第二个孩子I。

10）访问D的第三个孩子J。

先序遍历的结果为ABEFCGDHIJ。

（2）后序遍历

先后序遍历根结点的每一棵子树，然后再访问根结点，以图6-27为例：

1）访问根结点A的第一棵子树，访问子树时先访问根B的第一个孩子E。

2）访问B的第二个孩子F。(www.daowen.com)

3）访问B。

4）访问A的第二棵子树，访问子树时先访问根C的第一个孩子G。

5）访问C。

6）访问A的第三棵子树，访问子树时先访问根D的第一个孩子H。

7）访问D的第二个孩子I。

8）访问D的第三个孩子J。

9）访问D。

10）最后访问根结点A。

后序遍历的结果为EFBGCHIJDA。

树转换为二叉树后，树的先序遍历对应二叉树的先序遍历，树的后序遍历对应二叉树的中序遍历（注意不是后序遍历）。所以，可以将树转换为二叉树后，借助遍历二叉树的方法来遍历树。假如一棵树已经转化为二叉树来存储，要得到其先序遍历序列，只需先序遍历这棵二叉树；要得到其后序遍历序列，只需中序遍历这棵二叉树。

2.森林的遍历

森林的遍历方式有两种：先序遍历和后序遍历。

先序遍历的过程：先访问森林中第一棵树的根结点，然后先序遍历第一棵树中根结点的子树，最后先序遍历森林中除了第一棵树以外的其他树。

后序遍历的过程：后序遍历第一棵树中根结点的子树，然后访问第一棵树的根结点，最后后序遍历森林中除去第一棵树以后的森林。

如图6-25所示的森林，对其进行后序遍历的结果为：BCDA，FE，HJIG，其实就是对森林中的每一棵树分别进行后序遍历的结果。

将图6-25所示的森林转化为二叉树即得到图6-26。

对其进行中序遍历得到：BCDAFEHJIG，与森林的后序遍历序列相同。

森林转换为二叉树中，森林的先序遍历对应二叉树的先序遍历，森林的后序遍历对应二叉树的中序遍历。

注意：对于森林的第二种遍历方式，即本节中提到的森林的后序遍历，在不同的书或不同学校的考卷中有不同的表述方式，如有的就称其为森林的中序遍历。据笔者调查，更多的情况下描述成按森林的后序遍历，包括国外一些权威的教材和教学网站。因此这里大家要留心，对于考研数据结构，出现森林的中序和后序遍历，就当描述的是同一件事情即可。