前边提到的树的孩子兄弟存储结构是基于二叉链表实现的，即以二叉链表作为树的存储结构，只是结点中的指针域表示的意义不同，对比如下：

1）用二叉链表存储二叉树，结点中一个指针域叫作lchild，指向左孩子，另一个指针域叫作rchild，指向右孩子。

2）用二叉链表存储树，结点中一个指针（假设叫child）指向一个孩子，另一个指针（假设叫sibling）指向自己的兄弟结点。如图6-19所示，最左边是一棵树，最右边是这棵树转化为二叉树后存储在二叉链表中的情形。可以看到，A结点的child指向了自己的一个孩子B结点，A结点没有兄弟结点，因此sibling为空；再看B结点，B没有孩子结点，因此child为空，B的sibling指向了自己的兄弟结点C。因此，如果要找到A的孩子结点D，只需要A-＞child-＞sibling-＞sibling即可。

孩子兄弟存储结构实质上是一个二叉链表，用它来存储二叉树是最直观方便的，如何把一棵树也能方便地用孩子兄弟存储结构来存储呢？这就是本节的主要内容，将树转化为二叉树。图6-19所示即为将一棵树转化成二叉树，并存储在孩子兄弟存储结构中的过程。

以图6-19所示的树为例，将其转化为二叉树的过程如下：

1）将同一结点的各孩子结点用线（图6-20中的虚线所示）串起来，如图6-20所示。

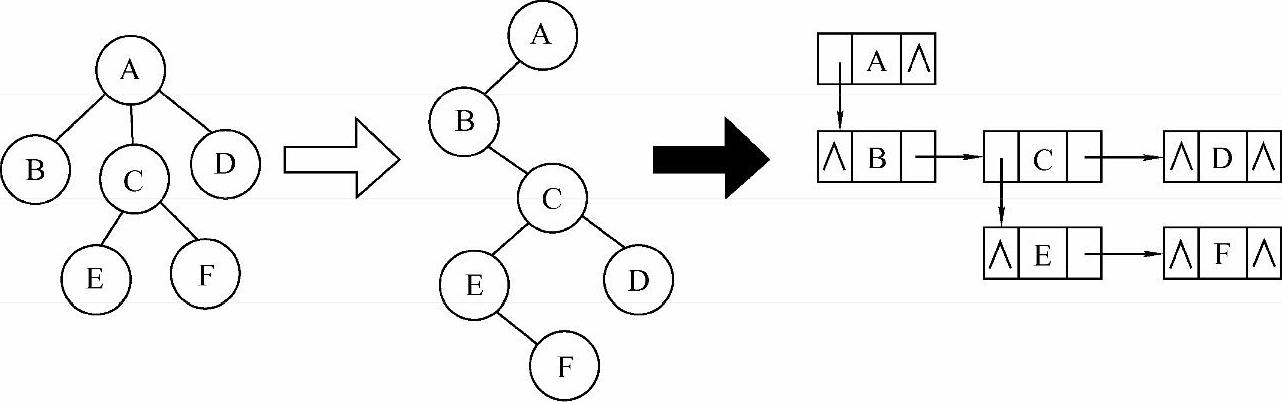
图6-19 将一棵树转化成二叉树并存储在孩子兄弟存储结构中

2）将每个结点的分支从左往右除了第一个以外，其余的都剪掉，如图6-21所示，即可得到如图6-22a所示的二叉树。

图6-20 将孩子结点串起来

(www.daowen.com)

图6-21 剪掉右侧结点的父子连线

3）调整结点使之符合二叉树的层次结构，如图6-22b所示。6.3.2 二叉树转换为树

掌握了树转化为二叉树的操作过程，这一节就比较简单了，只要把整个过程逆过来即可，具体过程如图6-23所示。

1）图6-23a所示是一棵二叉树，先把它从左上到右下分为若干层。如A是一层，B-C-D是一层，E-F是一层；然后调整成水平方向，如图6-23b所示。

2）找到每一层结点在其上一层的父结点。如第三层中，结点E、F在上一层的父结点为C，因为E和C相连；第二层中，结点B、C、D在上一层的父结点为A，因为B和A相连。

3）将每一层的结点和其父结点相连。如图6-23c中虚线所示；然后删除每一层结点之间的连接，如图6-23c中X号所示。最后得到的树如图6-23d所示。

图6-22 转换成的二叉树

a）调整前 b）调整后

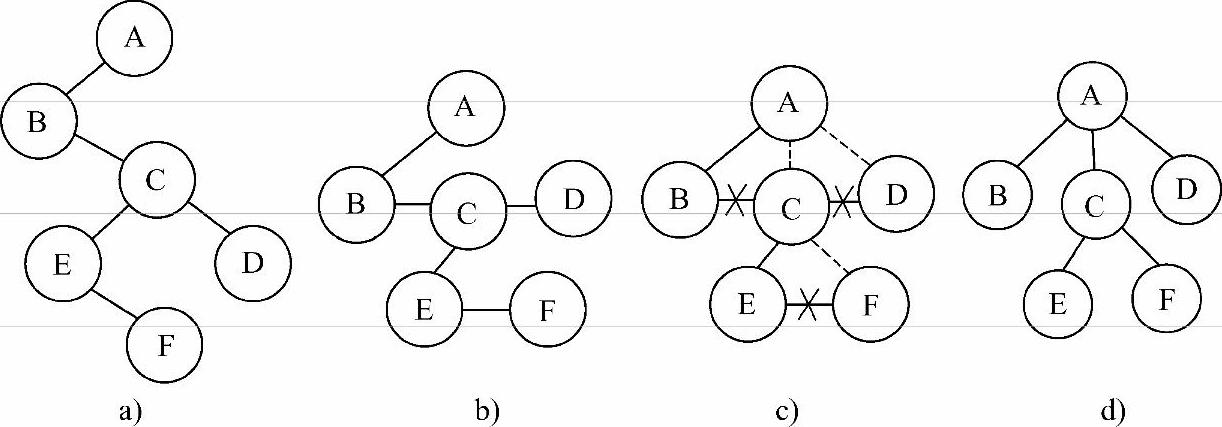
图6-23 二叉树转化为树的过程