上一节介绍的二叉树的深度优先遍历算法都是用递归函数实现的，这是很低效的，原因在于系统帮你调用了一个栈并做了诸如保护现场和恢复现场等复杂的操作，才使得遍历可以用非常简洁的代码实现。本节会介绍两种算法：二叉树深度优先遍历算法的非递归实现和线索二叉树。第一种算法用用户定义的栈来代替系统栈，也就是用非递归的方式来实现遍历算法，可以得到不小的效率提升；第二种算法将二叉树线索化，不需要栈来辅助完成遍历操作，更进一步提高了效率。

说明：有同学在平台问，关于二叉树深度优先遍历算法的非递归实现和递归实现，一个是用户自己定义栈，一个是系统栈，既然都用到栈，为什么用户自己定义的栈要比系统栈执行高效？一个较为通俗的解释是：递归函数所申请的系统栈，是一个所有递归函数都通用的栈。对于二叉树深度优先遍历算法，系统栈除了记录访问过的结点信息之外，还有其他信息需要记录，以实现函数的递归调用。用户自己定义的栈仅保存了遍历所需的结点信息，是对遍历算法的一个针对性的设计，对于遍历算法来说，显然要比递归函数通用的系统栈更高效。也就是一般情况下，专业的比通用的要好一些。

说明：在考研数据结构的视角下，所有相同功能的算法，如上述二叉树深度优先遍历算法，递归实现总是比非递归实现要低效。而实际应用中不是这样，如尾递归在很多机器上都会被优化为循环，因此递归函数不一定就比非递归函数执行效率低。同学们可以自行搜索下Recursio nv sLoop的相关话题，有很多精彩的讨论。

1.二叉树深度优先遍历算法的非递归实现

（1）先序遍历非递归算法

要写出其遍历的非递归算法，主要任务就是用自己定义的栈来代替系统栈的功能。栈在遍历过程中主要做了哪些事情呢？以图6-11所示的这棵二叉树为例，各个结点进栈、出栈过程如图6-12所示。

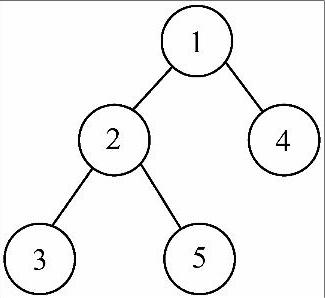
图6-11 示例二叉树

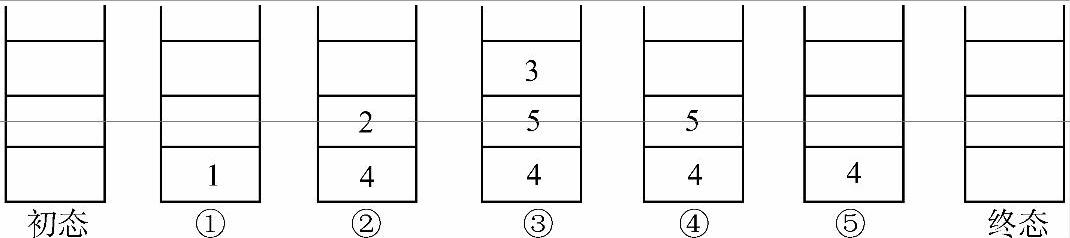
图6-12 先序遍历结点进出栈过程

初态栈空。

① 结点1入栈。

② 出栈，输出栈顶结点1，并将1的左、右孩子结点（2和4）入栈；右孩子先入栈，左孩子后入栈，因为对左孩子的访问要先于右孩子，后入栈的会先出栈访问。

③ 出栈，输出栈顶结点2，并将2的左、右孩子结点（3和5）入栈。

④ 出栈，输出栈顶结点3，3为叶子结点，无孩子，本步无结点入栈。

⑤ 出栈，输出栈顶结点5。

出栈，输出栈顶结点4，此时栈空，进入终态。

遍历序列为1，2，3，5，4。

由此可以写出以下代码：

（2）中序遍历非递归算法

类似于先序遍历，对图6-11中的二叉树进行中序遍历，各个结点进栈、出栈过程如图6-13所示。

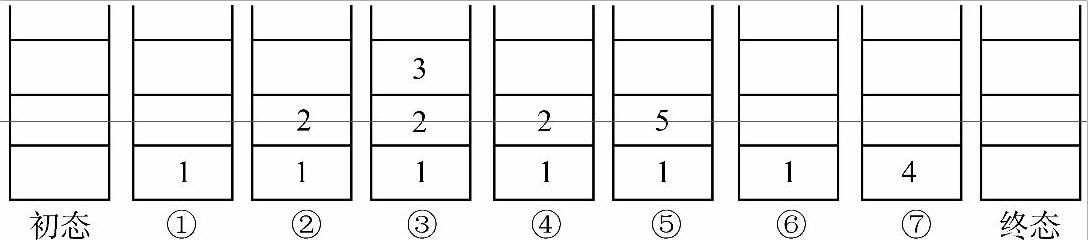
图6-13 中序遍历结点进出栈过程

初态栈空。

① 结点1入栈，1左孩子存在。

② 结点2入栈，2左孩子存在。

③ 结点3入栈，3左孩子不存在。

④ 出栈，输出栈顶结点3，3右孩子不存在。

⑤ 出栈，输出栈顶结点2，2右孩子存在，右孩子5入栈，5左孩子不存在。

⑥ 出栈，输出栈顶结点5，5右孩子不存在。

⑦ 出栈，输出栈顶结点1，1右孩子存在，右孩子4入栈，4左孩子不存在。

出栈，输出栈顶结点4，此时栈空，进入终态。

遍历序列为3，2，5，1，4。

由以上步骤可以看出，中序非递归遍历过程如下：

① 开始根结点入栈。

② 循环执行如下操作：如果栈顶结点左孩子存在，则左孩子入栈；如果栈顶结点左孩子不存在，则出栈并输出栈顶结点，然后检查其右孩子是否存在，如果存在，则右孩子入栈。

③ 当栈空时算法结束。

由此可以写出以下代码：

（3）后序遍历非递归算法

首先手工写出对图6-11中二叉树进行先序和后序遍历的序列。

先序遍历序列：1、2、3、5、4

后序遍历序列：3、5、2、4、1

把后序遍历序列逆序得：

逆后序遍历序列：1、4、2、5、3

观察发现，逆后序遍历序列和先序遍历序列有一定的联系，逆后序遍历序列只不过是先序遍历过程中对左右子树遍历顺序交换所得到的结果，如图6-14所示。

因此，只需要将前边讲到的非递归先序遍历算法中对左右子树的遍历顺序交换就可以得到逆后序遍历序列，然后将逆后序遍历序列逆序就得到了后序遍历序列。因此我们需要两个栈，一个栈stack1用来辅助做逆后序遍历（将先序遍历的左、右子树遍历顺序交换的遍历方式称为逆后序遍历）并将遍历结果序列压入另一个栈stack2，然后将stack2中的元素全部出栈，所得到的序列即为后序遍历序列。具体的进出栈过程如图6-15所示。

图6-14先序遍历序列和逆后序遍历序列的转化关系

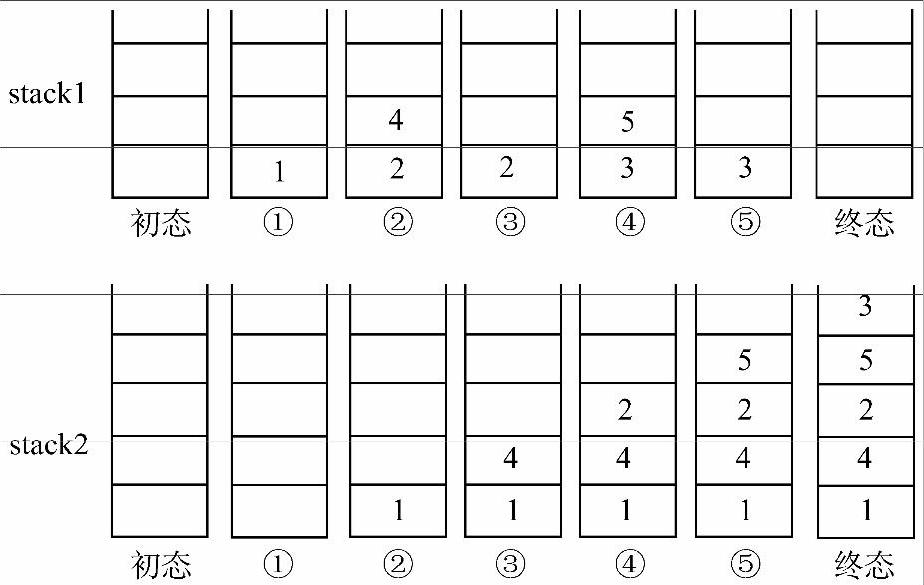
图6-15 后序遍历结点进出栈过程

初态栈空。

① 结点1入stack1。

② stack1元素出栈，并将出栈结点1入stack2，结点1的左、右孩子存在，左孩子结点2入stack1，右孩子结点4入stack1，这里注意和先序遍历进出栈过程对比，恰好是将其左、右孩子入栈顺序调换，以实现访问顺序的调换。

③ stack1元素出栈，并将出栈结点4入stack2，结点4的左、右孩子不存在。

④ stack1元素出栈，并将出栈结点2入stack2，结点2的左、右孩子存在，左孩子结点3入stack1，右孩子结点5入stack1。

⑤ stack1元素出栈，并将出栈结点5入stack2。

⑥ stack1元素出栈，并将出栈结点3入stack2。

此时stack1空，stack2中元素自顶向下依次为：3、5、2、4、1，正好为后序遍历序列。

由此可以写出以下代码：

(www.daowen.com)

说明：有同学提出，“上边的二叉树后序遍历非递归算法要用两个栈，空间复杂度貌似有点高，如何解决？”笔者的回答是，暂时不用解决，因为我们现在研究的是考研数据结构。在笔者调查的诸多真题中，在仅有的几道二叉树后序遍历非递归算法的考题中，均没有对空间复杂度的要求。原因是二叉树后序遍历非递归算法考题在考研数据结构中算是上等难度的题目，考生能够成功地将递归算法非递归化，已经算是达到了要求。非递归化的方法有很多，当然包括只用一个栈就能解决问题的方法。不过代码实现要比这个双栈法复杂且难理解得多。这里是基于考研数据结构的特点选取的一个最合适的算法。如有不满足于此的同学，可以自行去搜索一下其他的实现方法，有很多不错的代码。

2.线索二叉树

二叉树非递归遍历算法避免了系统栈的调用，提高了一定的执行效率。本节介绍的线索二叉树可以将用户栈也省掉，把二叉树的遍历过程线性化，进一步提高效率。

对于二叉链表存储结构，n个结点的二叉树有n+1个空链域，能不能把这些空链域有效地利用起来，以使二叉树的遍历更加高效呢？答案是肯定的，这就是线索二叉树的由来。在一般的二叉树中，我们只知道某个结点的左、右孩子，并不能知道某个结点在某种遍历方式下的直接前驱和直接后继，如果能够知道“前驱”和“后继”信息，就可以把二叉树看作一个链表结构，从而可以像遍历链表那样来遍历二叉树，进而提高效率。这对经常需要进行遍历操作的二叉树而言，无疑是很有用的。

说明：有同学在平台问，这里的高效具体体现在哪里？这个问题其实在考研真题中也出现过，可以做如下回答。

体现在：二叉树被线索化后近似于一个线性结构，分支结构的遍历操作就转化为了近似于线性结构的遍历操作，通过线索的辅助使得寻找当前结点前驱或者后继的平均效率大大提高。

说明：看到上边这个答案可能有些同学又要问：“栈都不需要了，并且将树中原有的空指针废物利用了起来，所以上边这个答案是否应该再加一条对空间利用率提高的回答？一般的效率相关问答题不都是从时间复杂度和空间复杂度两方面考虑吗？”原因是，每个结点中多了两个标识域ltag和rtag，它们导致的额外空间开销是否比非递归遍历算法中的栈空间开销少，在不同的场合下很难确定，因此这里不提空间利用率的提高。

（1）中序线索二叉树的构造

线索二叉树的结点结构如下：

在二叉树线索化的过程中会把树中的空指针利用起来作为寻找当前结点前驱或后继的线索，这样就出现了一个问题，即线索和树中原有指向孩子结点的指针无法区分。上边的结点设计就是为了区分这两类指针，其中，ltag和rtag为标识域，它们的具体意义如下：

1）如果ltag=0，则表示lchild为指针，指向结点的左孩子；如果ltag=1，则表示lchild为线索，指向结点的直接前驱。

2）如果rtag=0，则表示rchild为指针，指向结点的右孩子；如果rtag=1，则表示rchild为线索，指向结点的直接后继。

对应的线索二叉树的结点定义如下：

线索二叉树可以分为前序线索二叉树、中序线索二叉树和后序线索二叉树。对一棵二叉树中所有结点的空指针域按照某种遍历方式加线索的过程叫作线索化，被线索化了的二叉树称为线索二叉树。图6-16所示为中序线索二叉树及其二叉链表表示。

说明：在考研数据结构中，中序线索二叉树的考查最为频繁，前序次之，后序最少，因此这里重点讲中序线索二叉树的相关知识点，前序和后序线索二叉树只做简单介绍。

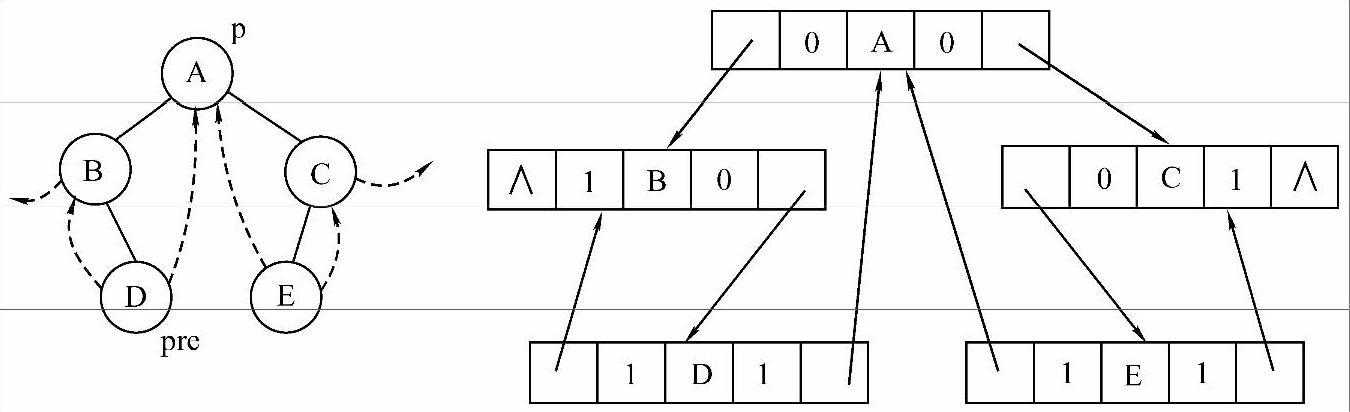
图6-16 中序线索二叉树及其二叉链表表示

二叉树中序线索化分析：

1）既然要对二叉树进行中序线索化，首先要有个中序遍历的框架，这里采用二叉树中序递归遍历算法，在遍历过程中连接上合适的线索即可。

2）线索化的规则是，左线索指针指向当前结点在中序遍历序列中的前驱结点，右线索指针指向后继结点。因此我们需要一个指针p指向当前正在访问的结点，pre指向p的前驱结点，p的左线索如果存在则让其指向pre，pre的右线索如果存在则让其指向p，因为p是pre的后继结点，这样就完成了一对线索的连接。如图6-16左图所示，某一时刻p指向A，pre指向了中序遍历过程中A的前驱D，A是D的后继，D的右线索存在则指向A。按照这样的规则一直进行下去，当整棵二叉树遍历完成的时候，线索化也就完成了。

3）上一步中保持pre始终指向p前驱的具体过程是，当p将要离开一个访问过的结点时，pre指向p；当p来到一个新结点时，pre显然指向的是此时p所指结点的前驱结点。

通过中序遍历对二叉树线索化的递归算法如下：

说明：

上一段代码中的如下3句：

是为了配合前边的讲解拆开写，方便理解，等你明白原理之后还是写成如下和递归遍历框架一致的形式比较好，方便老师阅卷。

通过中序遍历建立中序线索二叉树的主程序如下：

pre=p；

InThread（p-＞rchild，pre）；

（2）遍历中序线索二叉树

访问运算主要是为遍历中序线索二叉树服务的。这种遍历不再需要栈，因为它利用了隐含在线索二叉树中的前驱和后继信息。

求以p为根的中序线索二叉树中，中序序列下的第一个结点的算法如下：

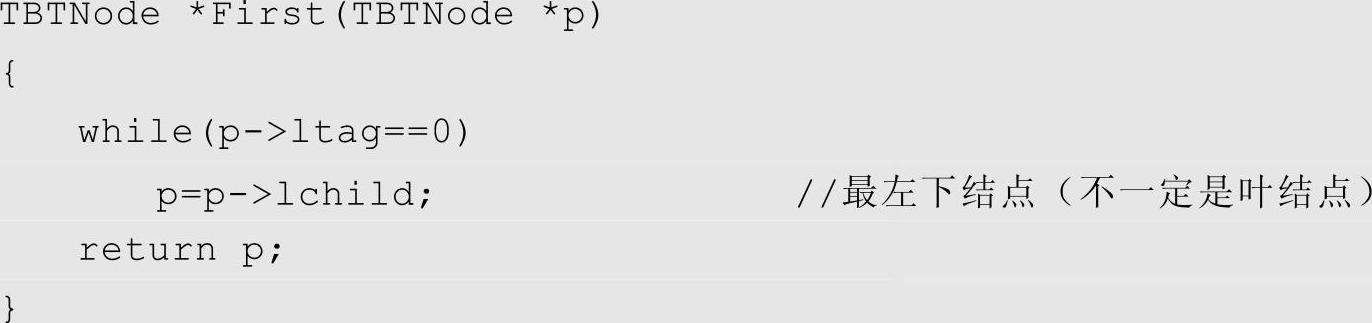
求在中序线索二叉树中，结点p在中序下的后继结点的算法如下：

如果把程序中First的ltag和lchild换成rtag和rchild，同时把函数名First换成Last，则可得到求中序序列下最后一个结点的函数Last（）；如果把程序中Next的rtag和rchild换成ltag和lchild，并同时把函数First（）换成函数Last（），再把函数名Next改为Prior则可得到求中序序列下前驱结点的函数Prior（）。

最后可以很容易地写出在中序线索二叉树上执行中序遍历的算法：

（3）前序线索二叉树

前序线索化代码和中序线索化代码极为相似，最大的区别就是把连接线索的代码提到了两递归入口前边，这也符合先序递归遍历的框架。

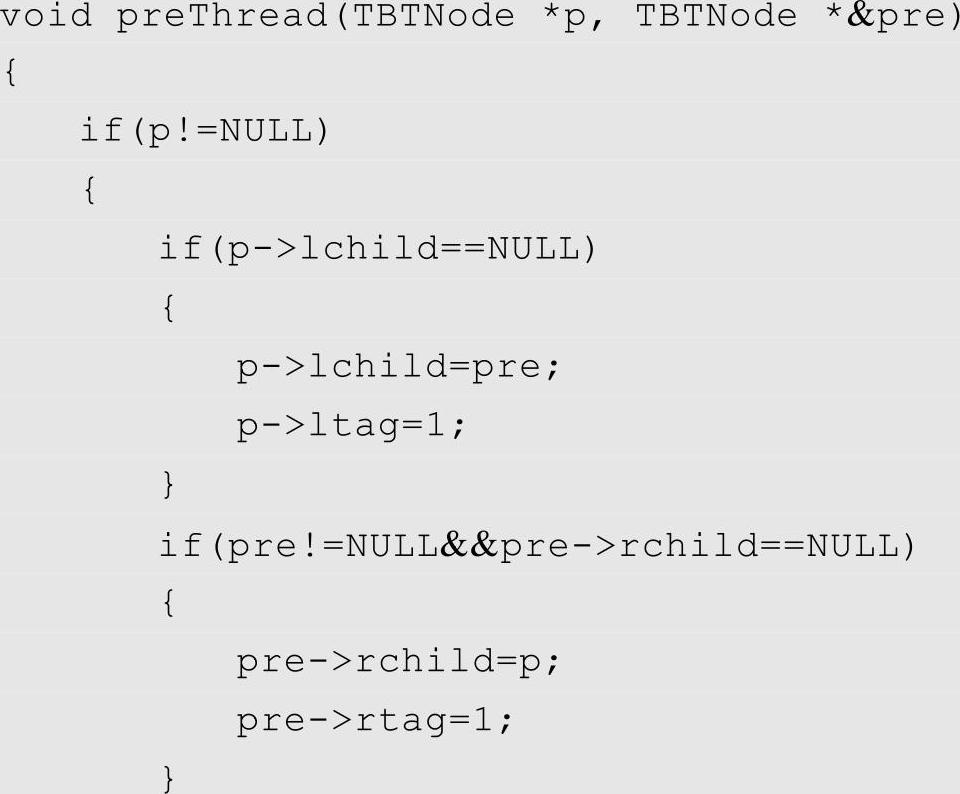
在前序线索二叉树上执行前序遍历的算法如下：

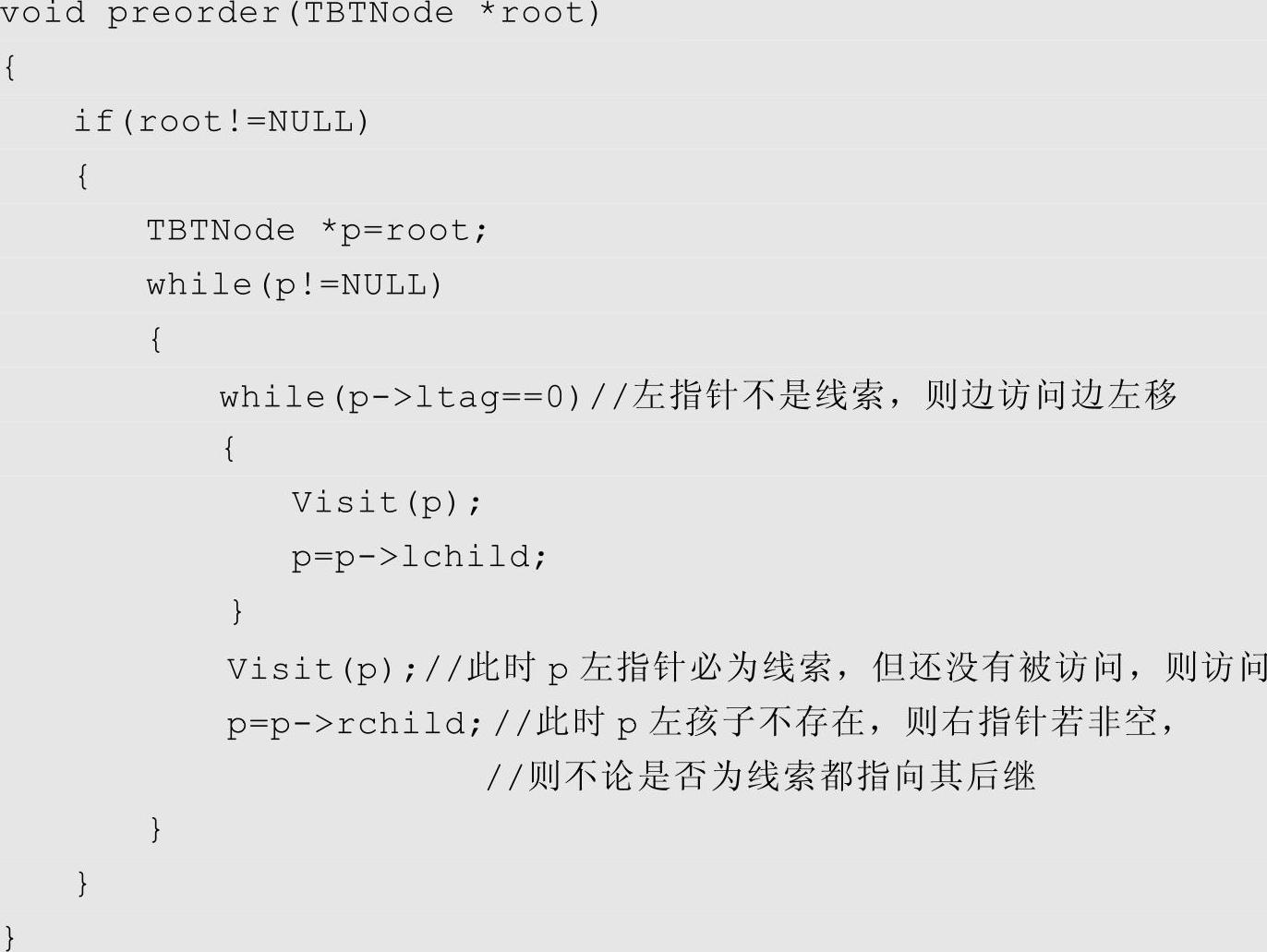
（4）后序线索二叉树

后序线索化代码和中序线索化代码极为相似，最大的区别就是把连接线索的代码放到了两递归入口后边，这也符合后序递归遍历的框架。

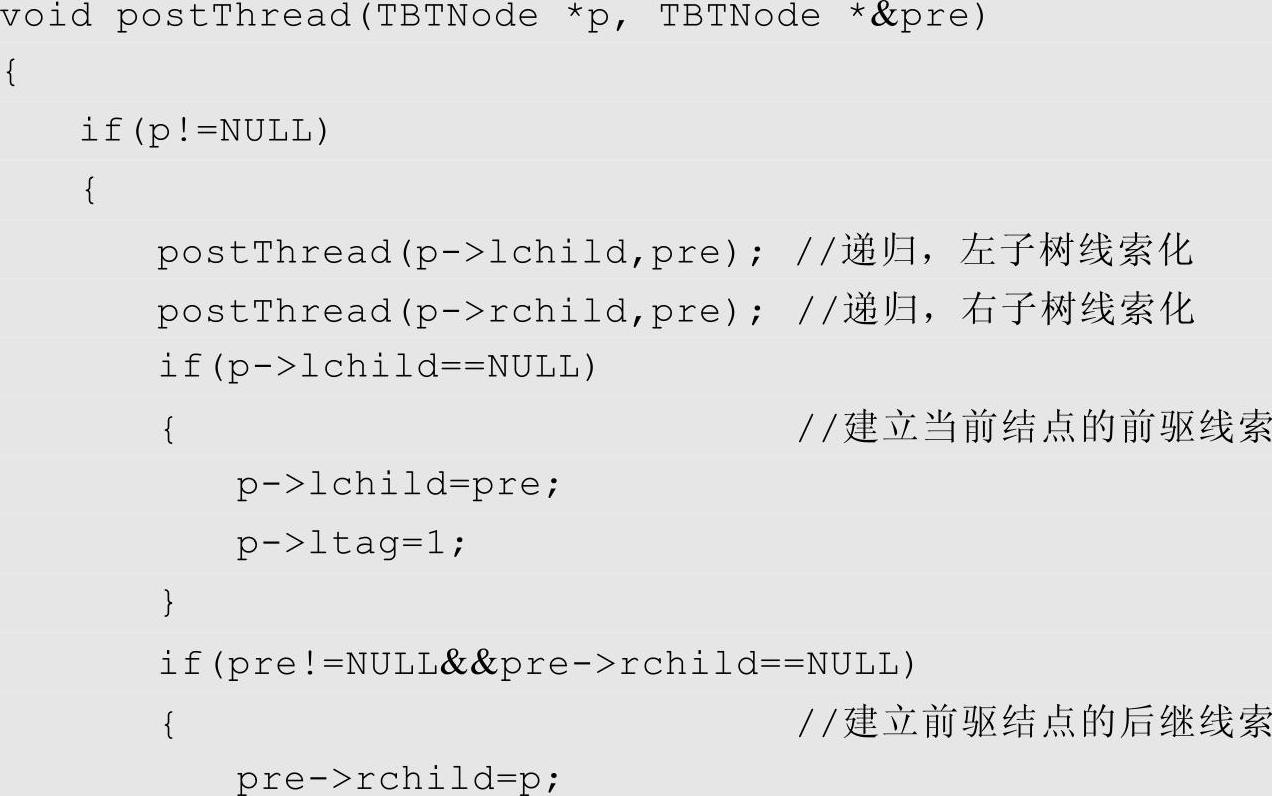
说明：对于后序线索二叉树的遍历，考研数据结构中出现的题目最多的是手工找出当前结点的后继，因此大家只需记住以下3点即可：

1）若结点x是二叉树的根，则其后继为空。

2）若结点x是其双亲的右孩子，或是其双亲的左孩子且其双亲没有右子树，则其后继即为双亲结点。

3）若结点x是其双亲的左孩子，且其双亲有右子树，则其后继为双亲右子树上按后序遍历列出的第一个结点。

说明：本节在考研数据结构选择题中涉及较多的是给出一棵二叉树，让考生指出其中一个结点的线索按照某种线索化方法所应该指向的结点。例如，请画出图6-17所示二叉树按照中序线索化方法线索化后，E结点的右线索的连接情况。解决这类题的方法为：先写出题目所要求的遍历方式下的结点访问序列，根据此序列找出题目要求中结点的前驱和后继，然后连接线索。图6-17所示二叉树的中序遍历序列为D，B，E，A，C。结点E的前驱为B，后继为A，因此其右线索应该指向A，结果如图6-18所示。

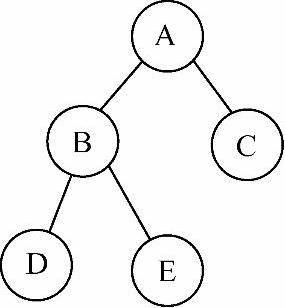
图6-17 示例二叉树

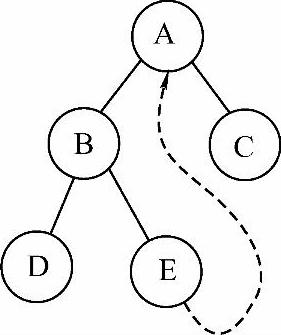
图6-18 示例二叉树的中序线索结果