为什么在二叉树所有的算法中要把遍历算法放在首位来讲呢？因为通过遍历一棵二叉树，就可得到这棵二叉树的所有信息，对这棵二叉树做最全面的了解。如果把一棵二叉树比作一个城市，想全面地了解这个城市，怎么做？最稳妥的方法就是你亲自走遍这个城市的每一个角落，对其做出细致的调查，即对这个城市进行遍历，这样就可以得到这个城市最全面的信息。例如，可以知道这个城市有多少个区，对应于二叉树中的结点数目；可以得到这个城市的规模，对应于二叉树的高度或者宽度（二叉树的宽度不是一个常见概念，在下面的例题中会讲到）等。

在考研中，主要用到的二叉树的遍历方式有先序遍历、中序遍历、后序遍历和层次遍历。很多算法题目都是基于这几种遍历方式而衍生出来的，因此只要能熟练掌握这些遍历方式，加之一定量的练习题，遇到考试中基于遍历的题目就都能迎刃而解。下面就对上述遍历方式逐一进行细致的讲解。

1.先序遍历

先序遍历的操作过程如下。

如果二叉树为空树，则什么都不做；否则：

1）访问根结点。

2）先序遍历左子树。

3）先序遍历右子树。

对应的算法描述如下：

2.中序遍历

中序遍历的操作过程如下。

如果二叉树为空树，则什么都不做；否则：

1）中序遍历左子树。

2）访问根结点。

3）中序遍历右子树。

对应的算法描述如下：

3.后序遍历

后序遍历的操作过程如下。

如果二叉树为空树，则什么都不做；否则：

1）后序遍历左子树。

2）后序遍历右子树。

3）访问根结点。

对应的算法描述如下：

说明：以上3种遍历方式以及算法描述都是简单易懂的，考生需要将它们作为模板来记忆，考研中的很多题目都是基于这3个模板而延伸出来的。

【例6-1】 表达式（a-（b+c））*（d/e）存储在图6-7所示的一棵以二叉链表为存储结构的二叉树中（二叉树结点的data域为字符型），编写程序求出该表达式的值（表达式中的操作数都是一位的整数）。

分析：

对于此题，该怎么用上述遍历方式来解决呢？假如这里有个表达式（A）*（B）（其中A、B均为表达式），如何求出它的值？一种可行的办法就是先求出A表达式的值，再求出B表达式的值，然后将两个表达式的值相乘就得到表达式（A）*（B）的值。

对于此题，可以将这棵二叉树分成3部分，如图6-8所示。

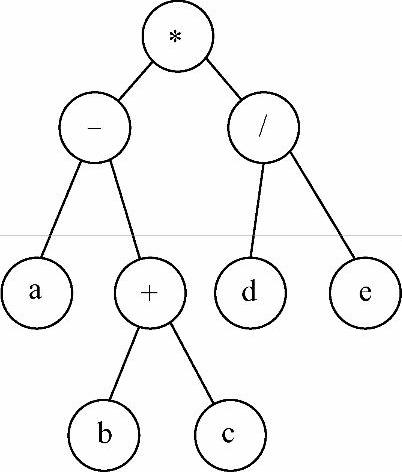
图6-7 例6-1图

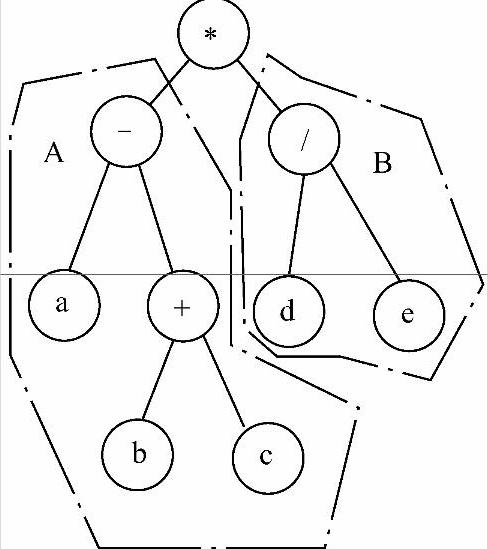
图6-8 二叉树分成3部分

左子树为表达式A，右子树为表达式B，经过上述分析可以这样求此表达式：先求左子树所表示的表达式的值，然后求右子树所表示的表达式的值，最后将两个结果相乘就是整个表达式的数值。这正对应于先遍历左子树（得左子树值），再遍历右子树（得右子树值），最后访问根（得运算符）的二叉树的后序遍历方式，因此可以采用后序遍历来解决此题。由此写出对应的程序代码如下：

说明：函数intop（intA，intB，charC）返回的是以C为运算符，以A、B为操作数的算式的数值。例如，若C为“+”，则返回A+B的值。

【例6-2】 写一个算法求一棵二叉树的深度，二叉树以二叉链表为存储方式。

分析：

假如已知一棵二叉树的左子树和右子树的深度，如何算出整棵树的深度呢？这是问题的关键。如果有一棵二叉树，左子树深度为LD，右子树深度为RD，则整棵树的深度就是max{LD，RD}+1，即左子树与右子树深度的最大值加上1，这个结论是显然的。因此这个求深度的过程就是先求左子树深度，再求右子树的深度，然后返回的两者之中的最大值加1就是整棵树的深度。这正对应于先遍历左子树（得到左子树的深度LD），再遍历右子树（得到右子树的深度RD），最后访问根（得到整棵树的深度为max{LD，RD}+1）的后序遍历方式。

由以上分析，可以写出对应的程序代码如下：

(www.daowen.com)

C语言基础补充：上述代码中的LD＞RD？LD：RD是一个三目运算符表达式，一般形式为A？B：C，其中A、B、C为3个表达式。如果A的值为真，则返回B的值，否则返回C的值。对于LD＞RD？LD：RD，如果LD＞RD，则返回LD的值，否则返回RD的值，即实现了求LD和RD两者最大值的目的。

【例6-3】 在一棵以二叉链表为存储结构的二叉树中，查找data域值等于key的结点是否存在（找到任何一个满足要求的结点即可），如果存在，则将q指向该结点，否则q赋值为NULL，假设data为int型。

分析：

因为题中二叉树各个结点data域的值没有任何规律，所以要判断是否存在data域值等于key的结点，必须按照某种方式把所有结点访问一遍，逐个判断其值是否为key。因此要用二叉树的遍历方式来解决此题，3种遍历方式都可以访问到二叉树中的所有结点，任选一种即可解题。这里选择先序遍历方式来解决此题。

由以上分析可写出如下程序代码：

说明：本题主要是让大家熟悉二叉树遍历代码的基本框架，如果要提高解决本题的效率，可以考虑这样一种改进策略，即当在左子树中找到满足要求的结点后，无须继续查找右子树，直接退出本层递归，这就是所谓的“剪枝操作”。由此可以写出如下代码：

重要技巧提示：

图6-9所示为指针p沿着图中箭头所指示路线游历整个二叉树的过程，并且对于图中每个结点，p都将经过它3次（如B结点周围的标号1、2和3，指出了p3次经过此结点的情况）。对应于p游历整棵树的过程的程序为图6-9中右边的程序模板。如果将对结点的访问操作写在（1）处，则是先序遍历，即对应于图中的每个结点，在p所走线路经过的标号1处（第一次经过这个结点时）对其进行访问；如果将对结点的访问操作写在（2）处，则是中序遍历，即对应于图中的每个结点，在标号2处（第二次经过这个结点时）对其进行访问；如果将对结点的访问操作写在（3）处，则是后序遍历，即对应于图中的每个结点，在标号3处（第三次经过这个结点时）对其进行访问。

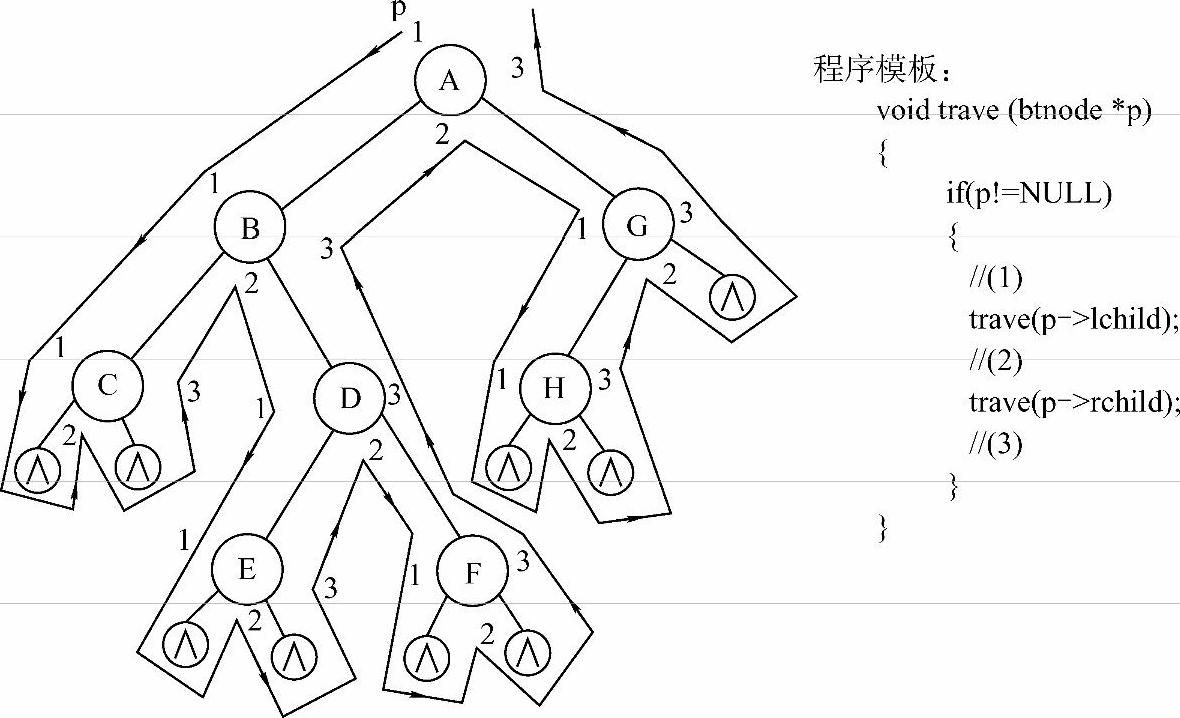
图6-9 二叉树遍历过程中指针p的行走路线及对应的程序模板

先序遍历输出序列为：A，B，C，D，E，F，G，H。

中序遍历输出序列为：C，B，E，D，F，A，H，G。

后序遍历输出序列为：C，E，F，D，B，H，G，A。

自己对应看一下，是否3种输出方式正好对应于图中p经过每个结点的不同次数时对其进行输出的结果（如后序遍历序列即为p沿着图中路线走到每个结点的3号处，即第3次走过此结点时进行输出的结果）。

以上提到的是一个十分重要的技巧，请考生务必理解并且牢记，这种技巧的应用在很多题目中都有体现。

补充：这里顺便提一个结论，即根据二叉树的前、中、后3种遍历序列中的前和中、中和后两对遍历序列都可以唯一确定这棵二叉树，而根据前和后这对遍历序列则不能确定这棵二叉树。

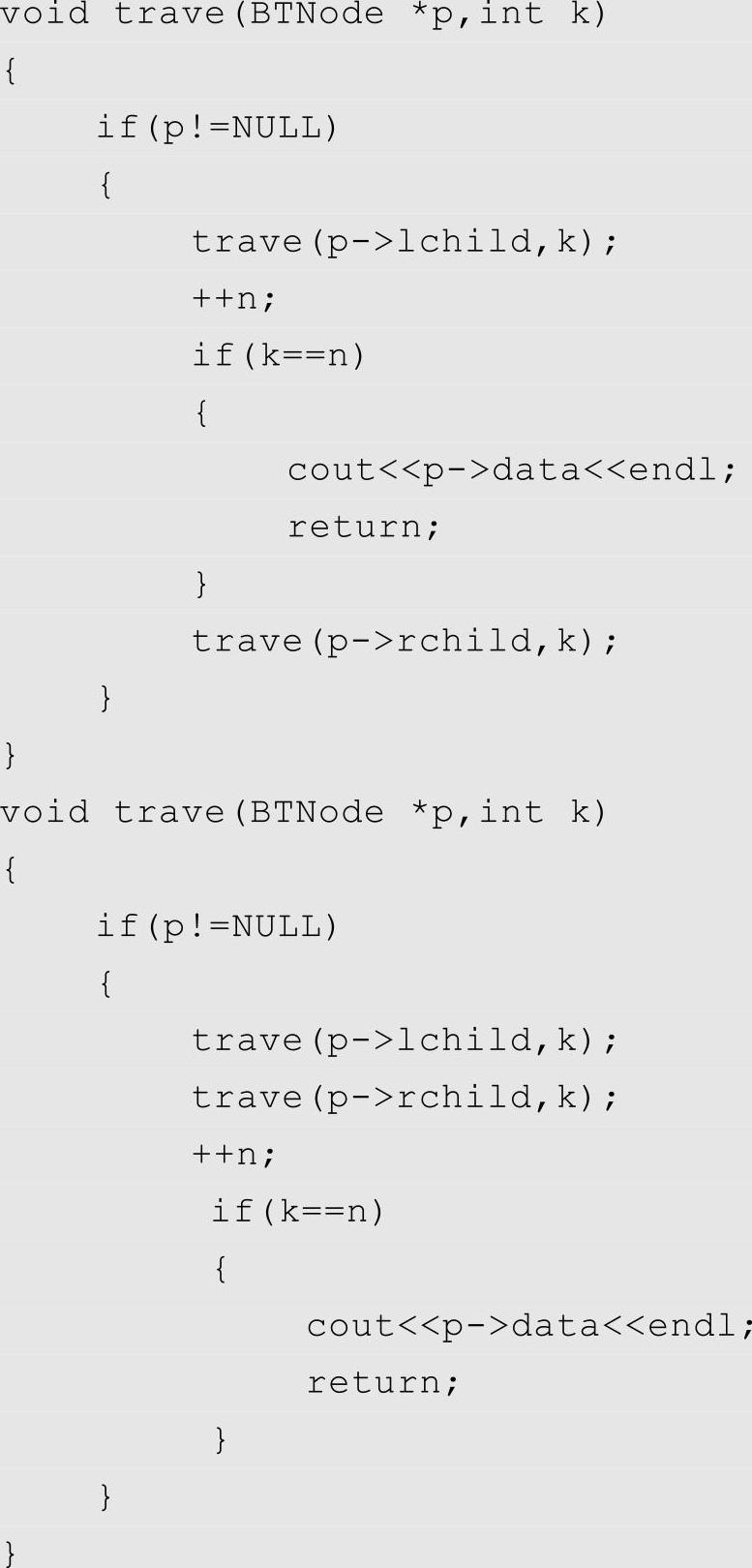
【例6-4】 假设二叉树采用二叉链表存储结构存储，编写一个程序，输出先序遍历序列中第k个结点的值，假设k不大于总的结点数（结点data域类型为char型）。

分析：

既然题目要求输出先序遍历序列中的第k个结点的值，由重要技巧提示可知，只需在上述程序模板中的（1）处添加代码，因为在此处添加代码意味着指针p第一次经过该结点时做出相应的操作。

由分析可写出以下程序代码：

倘若将题目中的先序改成中序或者后序，则可类似地写出如下程序代码：

4.层次遍历

图6-10所示为二叉树的层次遍历，即按照箭头所指方向，按照1、2、3、4的层次顺序，对二叉树中各个结点进行访问（此图反映的是自左至右的层次遍历，自右至左的方式类似）。

要进行层次遍历，需要建立一个循环队列。先将二叉树头结点入队列，然后出队列，访问该结点，如果它有左子树，则将左子树的根结点入队；如果它有右子树，则将右子树的根结点入队。然后出队列，对出队结点访问，如此反复，直到队列为空为止。

由此得到的对应算法如下：

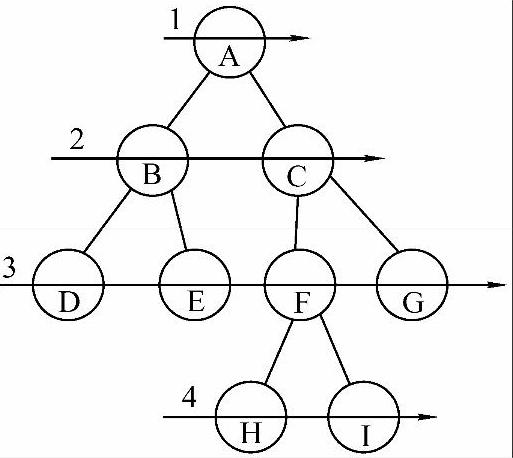
图6-10 二叉树的层次遍历

说明：对于上述二叉树层次的遍历算法，考生在复习中应该把它当作一个模板，在理解其执行过程的前提下记忆，并达到可以熟练默写的程度，这样才可以将这个层次遍历模型熟练应用于各种题目之中。下面通过几个基于层次遍历算法的题目来加深记忆，并掌握层次遍历的应用。

【例6-5】 假设二叉树采用二叉链表存储结构存储，设计一个算法，求出该二叉树的宽度（具有结点数最多的那一层上的结点个数）。

分析：

要求含有最大结点数的层上的结点数，可以分别求出每层的结点数，然后从中选出最大的。要达到这个目的，应该明白两个事实。

第一，对于非空树，树根所在的层为第一层，并且从层次遍历算法的程序中可以发现，有一个由当前结点找到其左、右孩子结点的操作。这就提示我们，如果知道当前结点的层号，就可以推出其左、右孩子的层号，即为当前结点层号加1，进而可以求出所有结点的层号。

第二，在层次遍历中，用到了一个循环队列（队列用数组表示），其出队和入队操作为front=（front+1）%maxSize；和rear=（rear+1）%maxSize；两句。如果用来存储队列的数组足够长，可以容纳树中所有结点，这时在整个遍历操作中队头和队尾指针不会出现折回数组起始位置的情况，那么front=（front+1）%maxSize；可以用++front；代替，rear=（rear+1）%maxSize；可以用++rear；代替。出队操作只是队头指针front后移了一位，但并没有把队头元素删除。在数组足够长的情况下，队头元素也不会被新入队的元素覆盖。

搞清了上边两件事情后，这个题目就好解决了。由第一点可以算出所有结点的层号。由第二点可以知道所访问的结点最终保存在数组里。因此只需修改层次遍历算法模板，在其中添加上求层号的操作，并且将循环队列的操作改为非循环队列的操作。在遍历结束后，数组中记录了树中所有结点的层号信息，进而可以求出含有结点最多的层上的结点数。

由此可以写出以下程序代码：