1.顺序存储结构

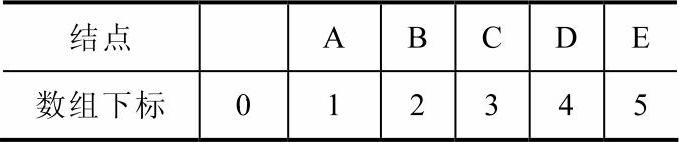
顺序存储结构即用一个数组来存储一棵二叉树，这种存储方式最适合于完全二叉树，用于存储一般二叉树会浪费大量的存储空间。将完全二叉树中的结点值按编号依次存入一个一维数组中，即完成了一棵二叉树的顺序存储。例如，将图6-5中所示的完全二叉树存入数组BTree[]中，见表6-1。

例如，知道了顶点A的下标为1，要得到A的左孩子结点只需访问BTree[1*2]即可。类似地，如果知道了一个结点i，如果2i不大于n，则i的左孩子结点就存在于BTree[2*i]内。

表6-1 数组BTree[]

2.链式存储结构

顺序存储结构显然有很大的局限性，不便于存储任意形态的二叉树。观察二叉树的形态可以发现是一个根结点与两棵子树之间的关系，因此设计出了含有一个数据域和两个指针域的链式结点结构，具体如下：(www.daowen.com)

其中，data表示数据域，用于存储对应的数据元素；lchild和rchild分别表示左指针域和右指针域，分别用于存储左孩子结点和右孩子结点的位置。这种存储结构又称为二叉链表存储结构，如图6-6所示。对应的结点类型的定义如下：

说明：考试中如果让写出结点定义，以上就是适用范围最广且最简的写法，可适用于要求用纯C或者C++来写代码的学校。其他书中可能还有其他的表示方法，为了简化记忆，只需要熟练掌握这一种写法，对考研要求已经足够了。有些题目可能需要在这个结构定义的基础上做一些修改，但万变不离其宗。

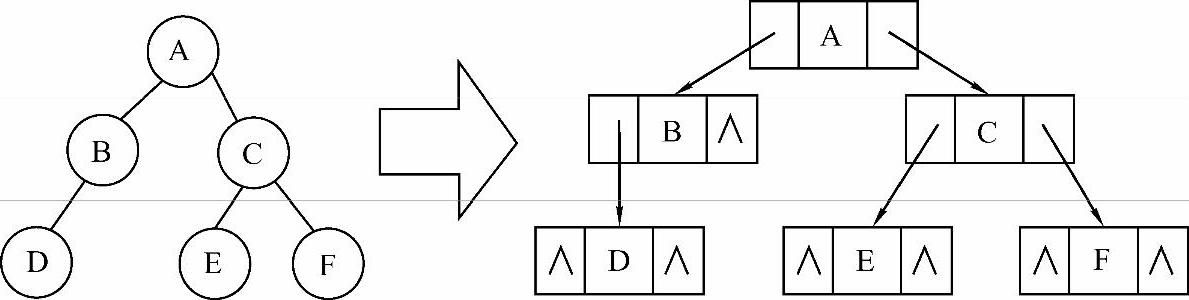
图6-6 二叉树以链式存储结构存储