性质1 非空二叉树上叶子结点数等于双分支结点数加1。

证明：设二叉树上叶子结点数为n₀，单分支结点数为n₁，双分支结点数为n₂，则总结点数为n₀+n₁+n₂。在一棵二叉树中，所有结点的分支数等于单分支结点数加上双分支结点数的两倍，即总的分支数为n₁+2n₂。

由于二叉树中除根结点之外，每个结点都有唯一的一个分支指向它，因此二叉树中有总分支数=总结点数-1（显然这一条结论对于任何树都是适用的，而不仅仅是针对二叉树）。

由此可得：n₀+n₁+n₂-1=n₁+2n₂

化简得：n₀=n₂+1

说明：这个性质在选择题中常有体现，并且需要灵活运用。例如，题目可能问二叉树中总的结点数为n，则树中空指针的个数是多少？可以将所有的空指针看作叶子结点，则树中原有的所有结点都成了双分支结点。因此可得空指针的个数为树中所有结点个数加1，即n+1个。

这个性质还可以扩展，即在一棵度为m的树中，度为1的结点数为n₁，度为2的结点数为n₂，…，度为m的结点数为n_m，则叶子结点数n₀=1+n₂+2n₃+…+（m-1）n_m。推导过程如下：

总结点数=n₀+n₁+n₂+…+n_m ①

总分支数=1×n₁+2×n₂+…+m×n_m（度为m的结点引出m条分支） ②

总分支数=总结点数-1 ③

将式①、式②代入式③并化简得

n₀=1+n₂+2n₃+…+（m-1）n_m

性质2二叉树的第i层上最多有2^i-1（i≥1）个结点。

结点最多的情况即为满二叉树的情况，此时二叉树每层上的结点数构成了一个首项为1、公比为2的等比数列。通项为2^i-1，i为层号。

性质3高度（或深度）为k的二叉树最多有2^k-1（k≥1）个结点。换句话说，满二叉树中前k层的结点个数为2^k-1。

其实本条性质描述的即为性质2中等比数列的前k项和的问题，由等比数列的求和公式可得结果，即（1-2^k）/（1-2）=2^k-1。

性质4有n个结点的完全二叉树，对各结点从上到下、从左到右依次编号（编号范围为1～n），则结点之间有如下关系。

若i为某结点a的编号，则：

如果i≠1，则a双亲结点的编号为[i/2]。

如果2i≤n，则a左孩子的编号为2i；如果2i＞n，则a无左孩子。

如果2i+1≤n，则a右孩子的编号为2i+1；如果2i+1＞n，则a无右孩子。

如图6-5所示，n为5，结点B编号为2，2×2=4＜5，因此编号为4的结点D为结点B的左孩子；2×2+1=5≤5，因此编号为5的结点E为结点B的右孩子。对于结点C，编号为3，因3×2=6＞5，因此结点C无左孩子。对于结点E，编号为5，[5/2]=2，即编号为2的结点B是其双亲结点。

注意：有些学校的考题中，编号从0开始，即A的编号为0，B的编号为1，以此类推。此时根据双亲结点编号求孩子结点编号和根据孩子结点编号求双亲结点编号的计算方法为：某结点a的编号为i，则其左孩子结点编号为2i+1，右孩子结点编号为2i+2；a的双亲结点编号为[i/2]-1。(www.daowen.com)

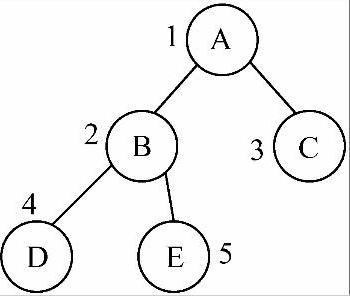
图6-5 有5个结点的完全二叉树

性质5 函数Catalan（）：给定n个结点，能构成h（n）种不同的二叉树，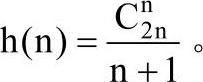

性质6 具有n（n≥1）个结点的完全二叉树的高度（或深度）为[log₂n]+1。

证明：由性质3可知：

2h^-1-1＜n≤2h-1，其中h为完全二叉树的高度。

又可以写为：

2^h-1≤n＜2^h

对其取对数得：

h-1≤log₂n＜h

由于h为整数，因此对log₂n向下取整即得到一个等式：

说明：

上述完全二叉树高度公式是在考研数据结构中出现最多的形式，但有些学校的考题中，尤其是选择题中给出的表达式是：

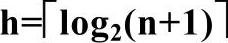
当然这个表达式也是对的，只是因推导过程中的等式选择不同，故产生的不同结果形式，下述是其推导过程：

将2^h-1-1＜n≤2^h-1，左、中、右全部加1得：

2^h-1＜n+1≤2^h

对其取对数得：

h-1＜log₂（n+1）≤h

由于h为整数，因此对log₂（n+1）向上取整即得到一个等式：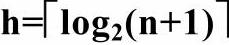

由于不同的学校对于推导过程中等式的不同选择或者对于树的高度的不同规定，会出现不同的高度表达式。因此希望同学们能掌握推导方法，而不仅是记住上述两个表达式的形式，这样在遇到其他形式的表达式时，能根据具体规定推导出正确的结果，进而分辨给出的表达式是否正确，这在某些选择题中是很有用的。