在理解了树的定义之后，二叉树的定义也就很好理解了。将一般的树加上如下两个限制条件就得到了二叉树。

1）每个结点最多只有两棵子树，即二叉树中结点的度只能为0、1、2。

2）子树有左右顺序之分，不能颠倒。

根据二叉树的定义，可以知道二叉树共有5种基本的形态，如图6-3所示。

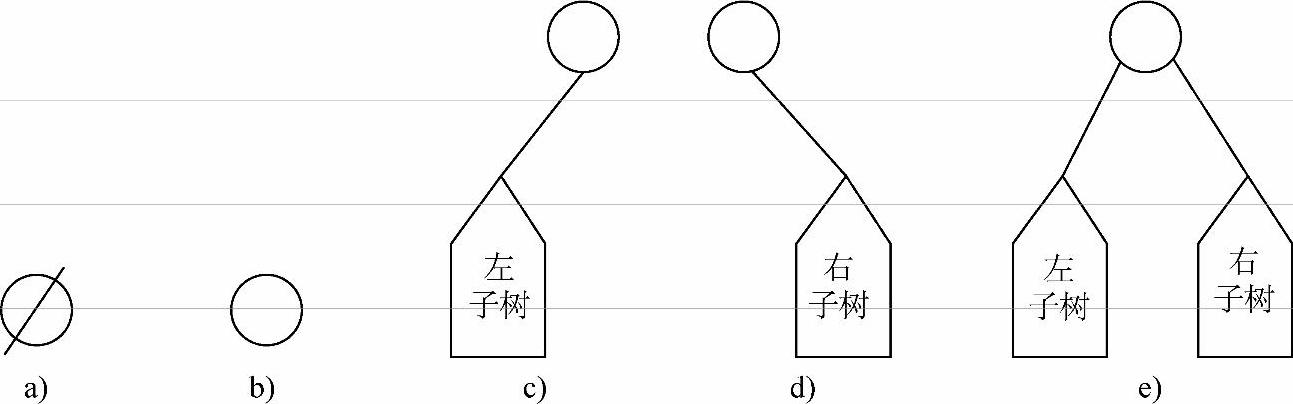
图6-3 二叉树的5种基本形态

a）空二叉树 b）只有根结点 c）只有左子树 d）只有右子树 e）左、右子树都有

二叉树的5种基本形态：

1）空二叉树（见图6-3a）。

2）只有根结点（见图6-3b）。(www.daowen.com)

3）只有左子树，右子树为空（见图6-3c）。

4）只有右子树，左子树为空（见图6-3d）。

5）既有左子树，又有右子树（见图6-3e）。

在一棵二叉树中，如果所有的分支结点都有左孩子和右孩子结点，并且叶子结点都集中在二叉树的最下一层，则这样的二叉树称为满二叉树。图6-4a所示就是一棵满二叉树。对满二叉树进行编号，约定编号从1开始，从上到下，自左至右进行，如图6-4a中各结点上方的数字所示。如果对一棵深度为k、有n个结点的二叉树进行编号后，各结点的编号与深度为k的满二叉树中相同位置上的结点的编号均相同，那么这棵二叉树就是一棵完全二叉树。

在图6-4b中，结点F用虚线画出。如果F存在于图6-4b所示的二叉树中，则F的编号为6，与图6-4a中满二叉树同一位置上的结点G的编号7不同，此时图6-4b中的二叉树就不是完全二叉树。如果F不存在于图6-4b所示的二叉树中，则图6-4b中二叉树的各个结点的编号与图6-4a中二叉树相同位置上的结点的编号均相同，此时图6-4b中的二叉树就是完全二叉树。

说明：通俗地说，一棵完全二叉树一定是由一棵满二叉树从右至左从下至上，挨个删除结点所得到的。如果跳着删除，则得到的不是完全二叉树。如图6-4a中，如果删除结点G和F，则得到一棵完全二叉树。如果跳着删除，即不删除G，直接删除F，则得到的不是完全二叉树。

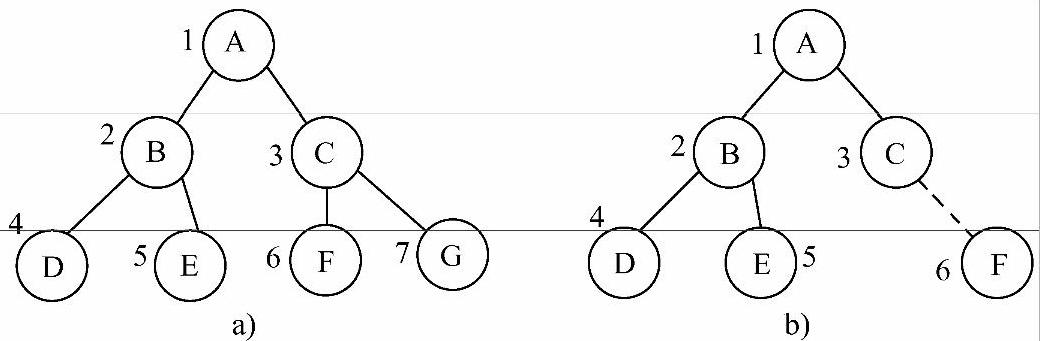
图6-4 满二叉树和完全二叉树

a）满二叉树 b）完全二叉树