用图6-1中的树作为例子。

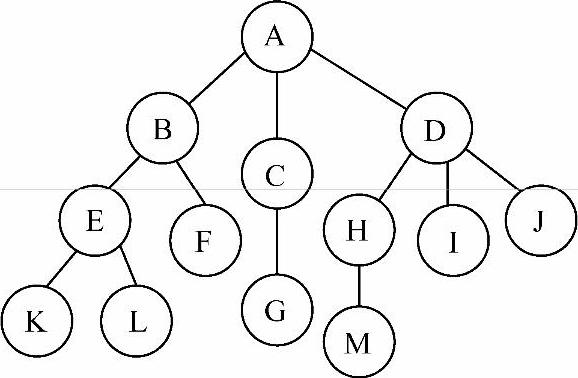
图6-1 树

结点：A、B、C等都是结点，结点不仅包含数据元素，而且包含指向子树的分支。例如，A结点不仅包含数据元素A，而且包含3个指向子树的指针。

结点的度：结点拥有的子树个数或者分支的个数。例如，A结点有3棵子树，所以A结点的度为3。

树的度：树中各结点度的最大值。如例子中结点度最大为3（A、D结点），最小为0（F、G、I、J、K、L、M结点），所以树的度为3。

叶子结点：又叫作终端结点，指度为0的结点，如F、G、I、J、K、L、M结点都是叶子结点。

非终端结点：又叫作分支结点，指度不为0的结点，如A、B、C、D、E、H结点都是非终端结点。除了根结点之外的非终端结点，也叫作内部结点，如B、C、D、E、H结点都是内部结点。

孩子：结点的子树的根，如A结点的孩子为B、C、D。

双亲：与孩子的定义对应，如B、C、D结点的双亲都是A。

兄弟：同一个双亲的孩子之间互为兄弟。如B、C、D互为兄弟，因为它们都是A结点的孩子。

祖先：从根到某结点的路径上的所有结点，都是这个结点的祖先。如K的祖先是A、B、E，因为从A到K的路径为A—B—E—K。

子孙：以某结点为根的子树中的所有结点，都是该结点的子孙。如D的子孙为H、I、J、M。(www.daowen.com)

层次：从根开始，根为第一层，根的孩子为第二层，根的孩子的孩子为第三层，以此类推。

树的高度（或者深度）：树中结点的最大层次。如例子中的树共有4层，所以高度为4。

结点的深度和高度：

1）结点的深度是从根结到该结点路径上的结点个数。

2）从某结点往下走可能到达多个叶子结点，对应了多条通往这些叶子结点的路径，其中最长的那条路径的长度即为该结点在树中的高度，如结点D的高度为3，就是从D到M的路径长度。

3）根结点的高度为树的高度，如结点A，其高度为4，是从A到K（L、M）这条路径的长度，也是整棵树的高度。

堂兄弟：双亲在同一层的结点互为堂兄弟。如G和H互为堂兄弟，因为G的双亲是C，H的双亲是D，C和D在同一层上。注意和兄弟的概念的区分。

有序树：树中结点的子树从左到右是有次序的，不能交换，这样的树叫作有序树。

无序树：树中结点的子树没有顺序，可以任意交换，这样的树叫作无序树。

丰满树：丰满树即理想平衡树，要求除最底层外，其他层都是满的。

森林：若干棵互不相交的树的集合。例子中如果把根A去掉，剩下的3棵子树互不相交，它们组成一个森林。

说明：上述这些基本概念无须刻意地去记忆，根据例子理解即可。考研中一般不会就概念考概念，都是通过具体的题目来考查的。因此，在后面的讲解或者做题过程中如出现不熟悉的概念，回来查一下即可，题目做多了自然就记住了。