一句话概括广义表：表元素可以是原子或者广义表的一种线性表的扩展结构。

下面列举一些广义表的例子：

1）A=（ ），A是一个空表，长度为0，深度为1。

2）B=（d，e），B的元素全是原子，即d和e，长度为2，深度为1。

3）C=（b，（c，d）），C有两个元素，分别是原子b和另一个广义表（c，d），长度为2，深度为2。

4）D=（B，C），D的元素全是广义表，即B和C，长度为2，深度为3，由此可见，一个广义表的子表可以是其他已经定义的广义表的引用。

5）E=（a，E），E有两个元素，分别是原子a和它本身，长度为2，由此可见一个广义表可以是递归定义的。展开E可以得到（a，（a，（a，（a，…）））），是一个无限深的广义表。

由1）到5）可以总结出广义表的长度和深度求法，这是考试中遇到最多的题目类型。

广义表的长度：为表中最上层元素的个数，如广义表C长度为2，注意不是3。(www.daowen.com)

广义表的深度：为表中括号的最大层数。注意，求深度时需要将子表展开，如广义表D应该展开为（（d，e），（b，（c，d））），深度为3。

表头（Head）和表尾（Tail）：当广义表非空时，第一个元素为广义表的表头，其余元素组成的表是广义表的表尾。

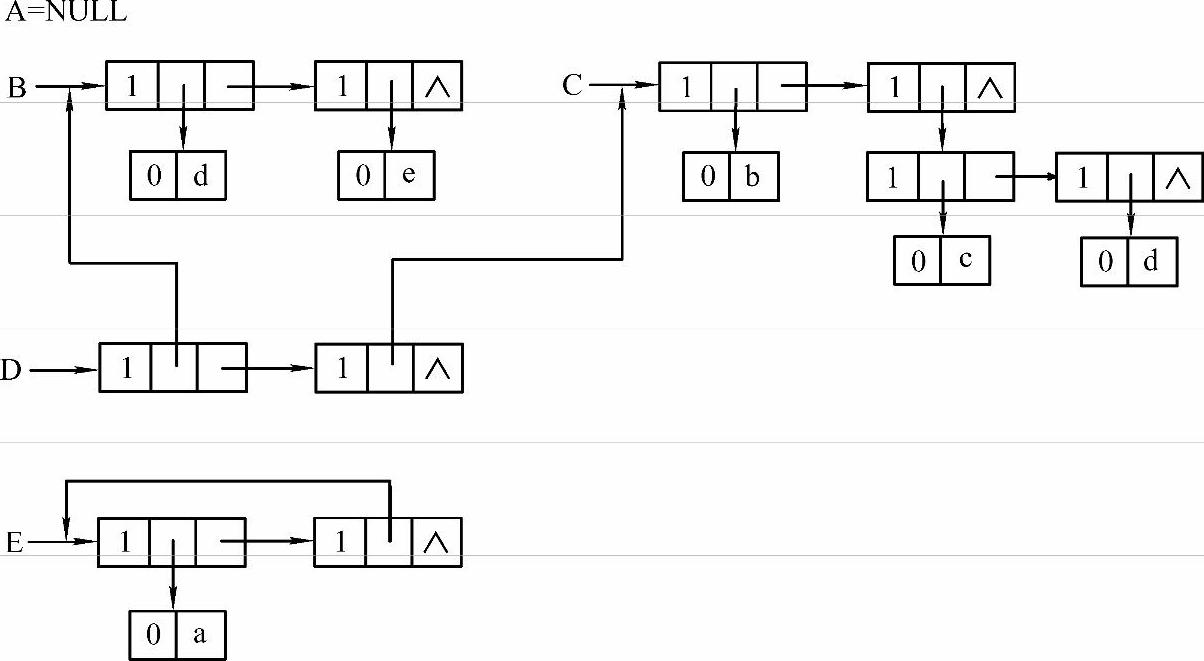
图5-7 广义表头尾链表存储结构

图5-7展示了1）到5）中广义表的头尾链表存储结构的存储情况，其中有两种结点，即原子结点和广义表结点。原子结点有两个域：标记域和数据域；广义表结点有3个域：标记域、头指针域与尾指针域。其中，标记域用于区分当前结点是原子（用0来表示）还是广义表（用1来表示），头指针域指向原子或者广义表结点，尾指针域为空或者指向本层中的下一个广义表结点。

图5-8展示了1）到5）中广义表的扩展线性表存储结构的存储情况，其中也有两种结点，即原子结点和广义表结点，不同的是原子结点有3个域：标记域、数据域和尾指针域；广义表结点也有3个域：标记域、头指针域与尾指针域。其中，标记域用于区分当前结点是原子（用0来表示），还是广义表（用1来表示）。这种存储结构类似于带头结点的单链表存储结构（而上一种类似于不带头结点的单链表存储结构），每一个子表都有一个不存储信息的头结点来标记其存在。

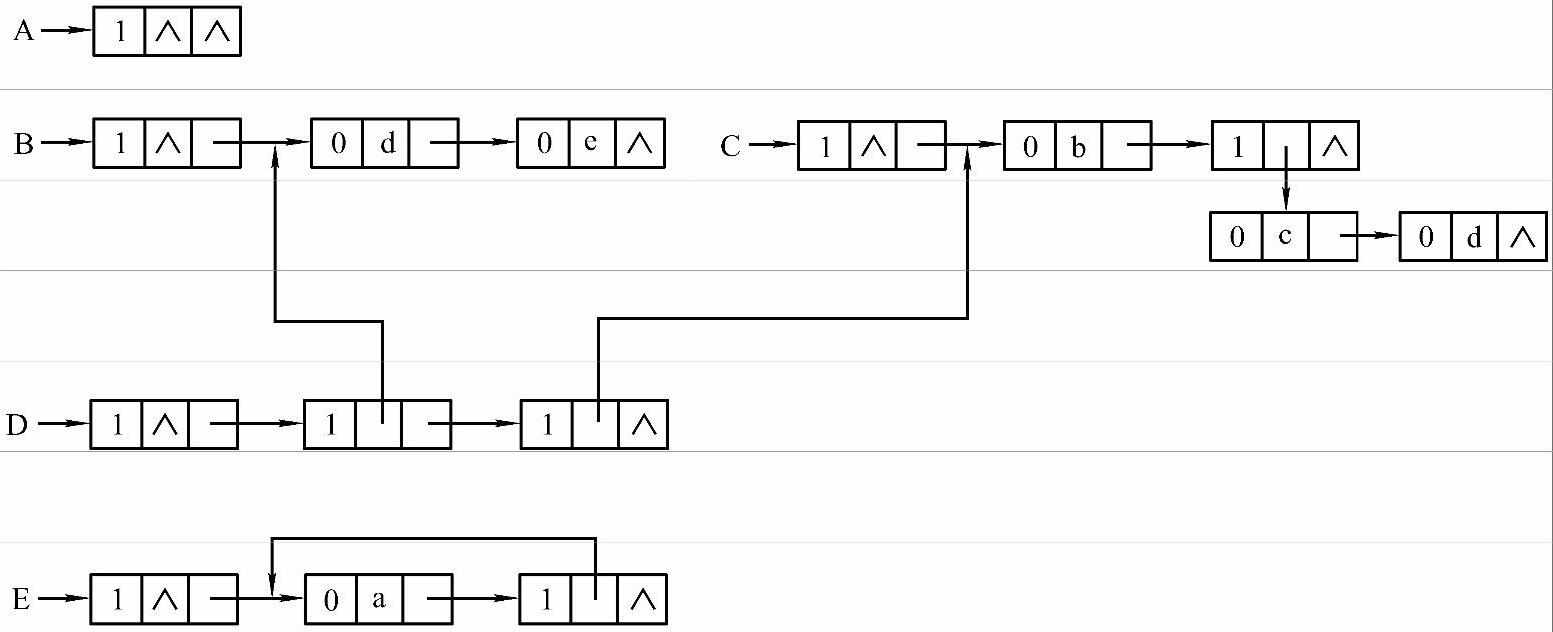
图5-8 广义表扩展线性表存储结构