相同的元素或者零元素在矩阵中的分布存在一定规律的矩阵称为特殊矩阵，反之称为稀疏矩阵。

注意：这个稀疏矩阵的定义是严版数据结构中给出的。对此我是不太认同的，国外普遍的对稀疏矩阵的定义是：矩阵中绝大多数元素都为0的矩阵为稀疏矩阵。既然我们关心的是考研数据结构，就要看你报考的学校对这个定义认不认同了，请查阅自己目标学校的推荐参考书和历年考题，以他们的定义为准。

1.特殊矩阵

这里主要介绍三种最常见的特殊矩阵。

（1）对称矩阵

矩阵中的元素满足a_i，j=a_j，i的矩阵称为对称矩阵，下面看一个关于对称矩阵的常见题型。

【例5-2】 假设有一个n×n的对称矩阵，第一个元素为a_0，0，请用一种存储效率较高的存储方式将其存储在一维数组中。

分析：

由对称矩阵a_i，j=a_j，i的性质可知其主对角线上下方元素对称相等，所以相同元素只需保存一份即可，所需的存储空间为（1+n）×n/2个。需要保存的元素为：

按照行优先来存储，保存在一维数组中的结果见表5-1。

表5-1 对称矩阵在一维数组中的表示

注意：这里有几个关键位置的元素下标必须计算出来。

1）第一个元素a_0，0的下标，显然为0。

2）左下角元素a_n-1，0，因为其上方有n-1行，每行元素个数构成等差数列，所以总个数为n×（n-1）/2个，因此a_n-1，0是第n×（n-1）/2+1个元素；又因为第k个元素在一维数组中的下标为k-1，所以a_n-1，0的下标为n×（n-1）/2。

3）右下角元素a_n-1，n_-1，用2）中类似的方法可算出为（1+n）×n/2-1。

其余元素可以这几个关键元素为参考系，配合省略号，适当标出几个，以表示所有元素在一维数组中的分布情况即可。

（2）三角阵

上三角阵为矩阵下三角部分（不包括对角线）元素全为c（c可为0）的矩阵。

下三角阵为矩阵上三角部分（不包括对角线）元素全为c（c可为0）的矩阵。

三角矩阵的存储方式和对称矩阵类似，以下三角矩阵为例，只需存储对角线及其以下部分的元素和其上三角中的一个元素c即可。如例5-2，假如其上三角部分元素全为c，则其在一维数组中的存储结果见表5-2。

表5-2 下三角阵在一维数组中的表示

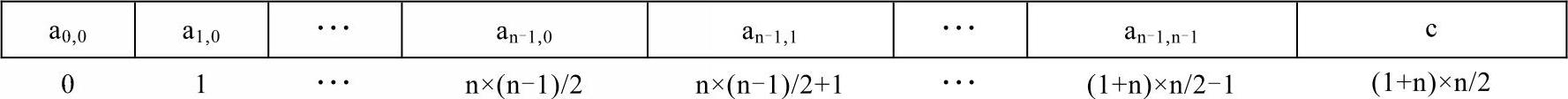
可见其结果仅仅比例5-2的结果多了一列。

（3）对角矩阵

图5-2所示为一个三对角矩阵，其特点是除主对角线以及其上下两条带状区域内的元素外，其余元素皆为c（c可为0）。

【例5-3】 对于图5-2中的三对角矩阵，求出第i行带状区域内的第一个元素在一维数组中的下标，假设c存在数组最后一位。

1）当i等于1时，带状区域内的第一个元素为矩阵中的第一个元素，其在一维数组中的下标为0。

图5-2 三对角矩阵

2）当i大于1时，第i行之前的元素个数为2+（i-2）×3，则带状区域内的第一个元素在一维数组中的下标为2+（i-2）×3。

2.稀疏矩阵

稀疏矩阵中的相同元素c（假设c为0）在矩阵中的分布不像在特殊矩阵中那么有规律可循，因此必须为其设计一些特殊的存储结构。

（1）稀疏矩阵的顺序存储及相关操作

常用的稀疏矩阵顺序存储方法有三元组表示法和伪地址表示法。

1）三元组表示法。

三元组数据结构为一个长度为n，表内每个元素都有3个分量的线性表，其3个分量分别为值、行下标和列下标。元素结构体定义如下：

在程序中如果要定义一个含有maxterms个非零元素的稀疏矩阵，则只需写成如下代码：

Trimat trimat[maxterms+1]；//maxterms是已经定义的常量

语句trimat[k].val；表示取第k个非零元素的值；trimat[k].i和trimat[k].j表示取第k个非零元素在矩阵中的行下标和列下标。

为了简便起见，可以不使用上述结构体定义的方法来定义三元组，直接申请一个如下的数组即可：

trimat[k][0]表示原矩阵中的元素按行优先顺序的第k个非零元素的值；trimat[k][1]、trimat[k][2]表示第k个非零元素在矩阵中的位置。可以看出trimat此时是一个maxterms行3列的数组，我们规定第0行的3个元素分别用来存储非零元素个数、行数和列数。例如，语句trimat[0][0]为原矩阵中的非零元素个数，trimat[0][1]和trimat[0][2]为矩阵行数和列数。(www.daowen.com)

说明：如果矩阵中元素是float型（或者其他非整型数据类型），则此时用一个数组来表示三元组要写成如下形式：

floattrimat[maxterms+1][3]；

这样会带来一个问题：非零元素在矩阵中的行号和列号也被表示成了float型，本应是int型。这在很多情况下会出现问题，因此严格来说，取当前非零元素在矩阵中的位置应写成如下语句：

（int）trimat[k][1]；

（int）trimat[k][2]；

上面用强制类型转换来实现取位置的操作，简单地说，就是将float型的行号和列号变量转换成了int型。

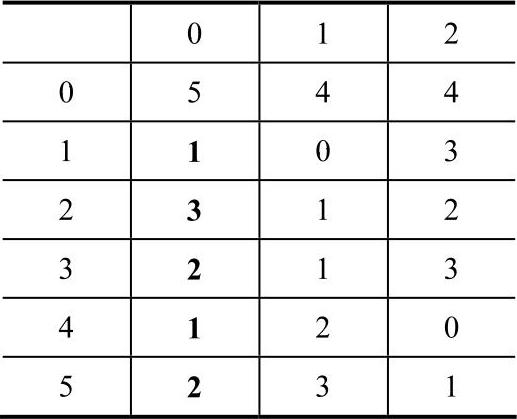
图5-3所示为一个4×4的稀疏矩阵A，该矩阵的三元组表示见表5-3。

【例5-4】 给定一个稀疏矩阵A（float型），其尺寸为m×n，建立其对应的三元组存储，并通过三元组打印输出矩阵A。

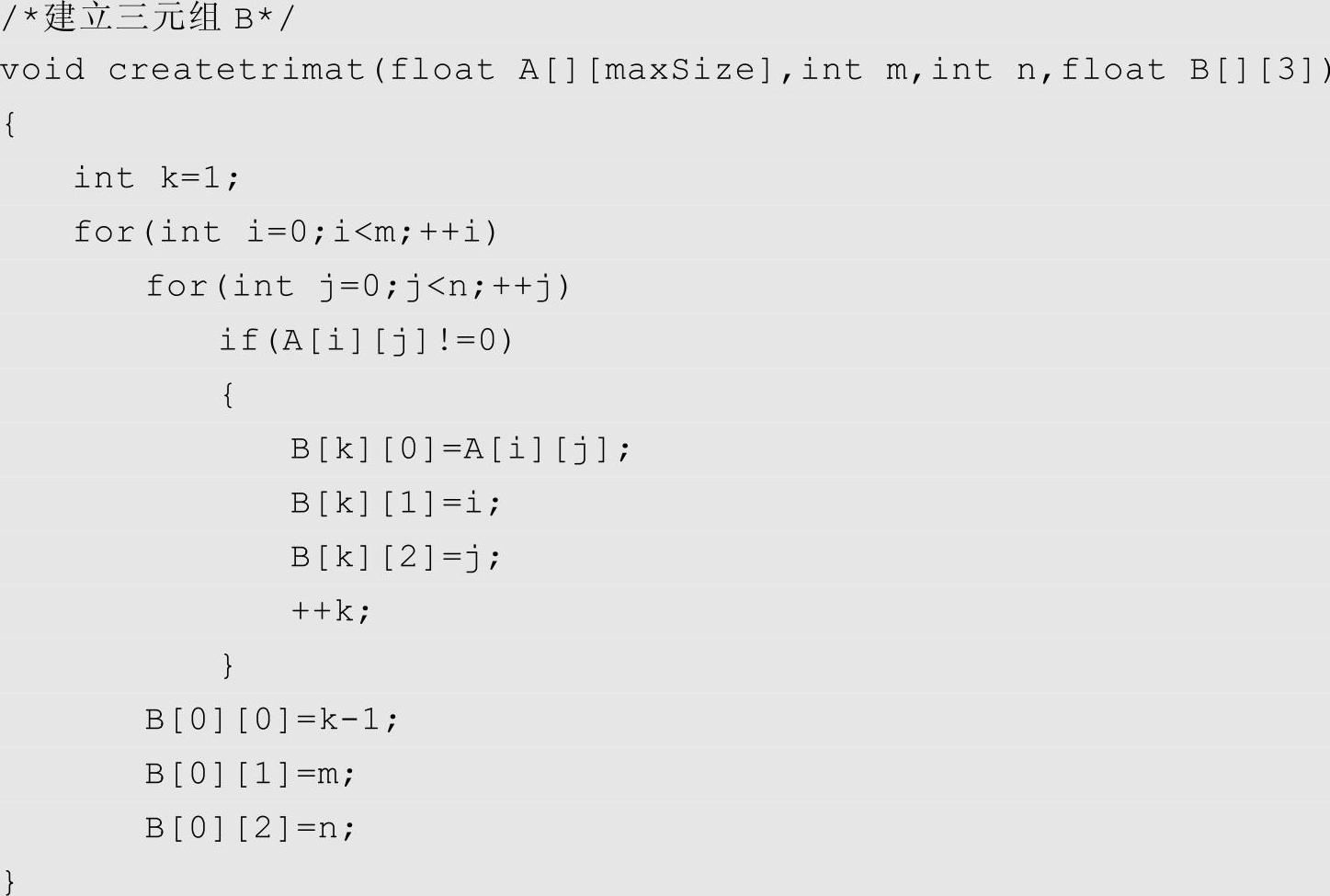
算法分析：建立一个三元组的核心问题在于求原矩阵的非零元素个数、非零元素的值，以及非零元素在原数组中的位置。本题算法较简单，扫描矩阵A即可得到相关数据，进而建立三元组，名为B，最后进行打印。具体实现代码如下：

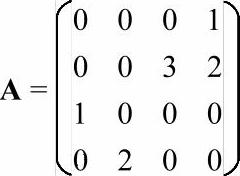
图5-3 一个稀疏矩阵A

表5-3 矩阵A的三元组表示

注意：建立三元组的时候，结点间的次序按元素在矩阵中的行优先顺序排列。

2）伪地址表示法。

伪地址即元素在矩阵中按照行优先或者列优先存储的相对位置。用伪地址方法存储稀疏矩阵和三元组方法相似，只是三元组每一行中有两个存储单元存放地址，而伪地址法只需要一个，因此伪地址法每一行只有两个存储单元，一个用来存放矩阵元素值，另一个用来存放伪地址。这种方法需要2N个存储单元，N为非零元素个数，对于一个m×n的稀疏矩阵A，元素A[i][j]的伪地址计算方法为n（i-1）+j。根据这个公式，不仅可以计算矩阵中一个给定元素的伪地址，还可以反推出给定元素在原矩阵中的真实地址。

（2）稀疏矩阵的链式存储及相关操作

在稀疏矩阵的链式存储方法中，最常用的有两种：邻接表表示法和十字链表表示法。

1）邻接表表示法。

邻接表表示法将矩阵中每一行的非零元素串连成一个链表，链表结点中有两个分量，分别表示该结点对应的元素值及其列号。

对于矩阵A（见图5-3），用邻接表表示如图5-4所示。

说明：这里的邻接表和第7章中图的邻接表是同一个东西，类比来看，图的邻接矩阵相当于这里的原矩阵，图的邻接表相当于这里的邻接表，因此可以发现，之所以要开发图的邻接表存储，也是出于一种节约空间的考量。

2）十字链表表示法。

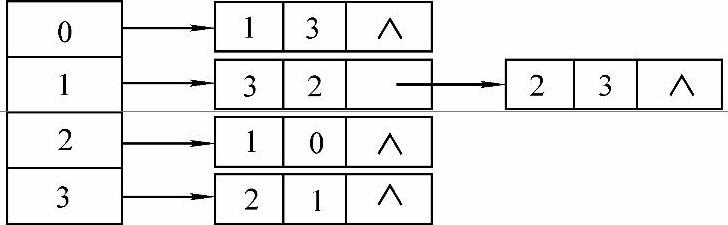
图5-4 稀疏矩阵的邻接表表示

在稀疏矩阵的十字链表存储结构中，矩阵的每一行用一个带头结点的链表表示，每一列也用一个带头结点的链表表示，这种存储结构中的链表结点都有5个分量：行分量、列分量、数据域分量、指向下方结点的指针、指向右方结点的指针。图5-5所示为十字链表结点结构图。

十字链表存储结构比较复杂，为了更形象地介绍，这里先给出图5-3中矩阵A的十字链表示意图，如图5-6所示。十字链表是由一些单链表纵横交织而成的，其中最左边和最上边是头结点数组，不存储数据信息，左上角的结点可以视为整个十字链表的头结点，它有5个分量，分别存储矩阵的行数、列数、非零元素个数以及指向两个头结点数组的指针。十字链表结点中除头结点以外的结点就是存储矩阵非零元素相关信息的普通结点。

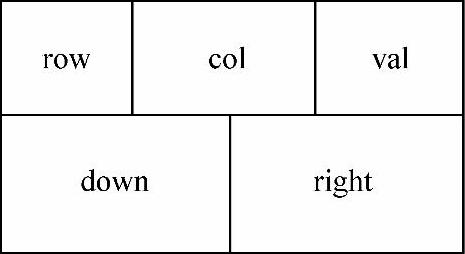
图5-5 十字链表结点结构图

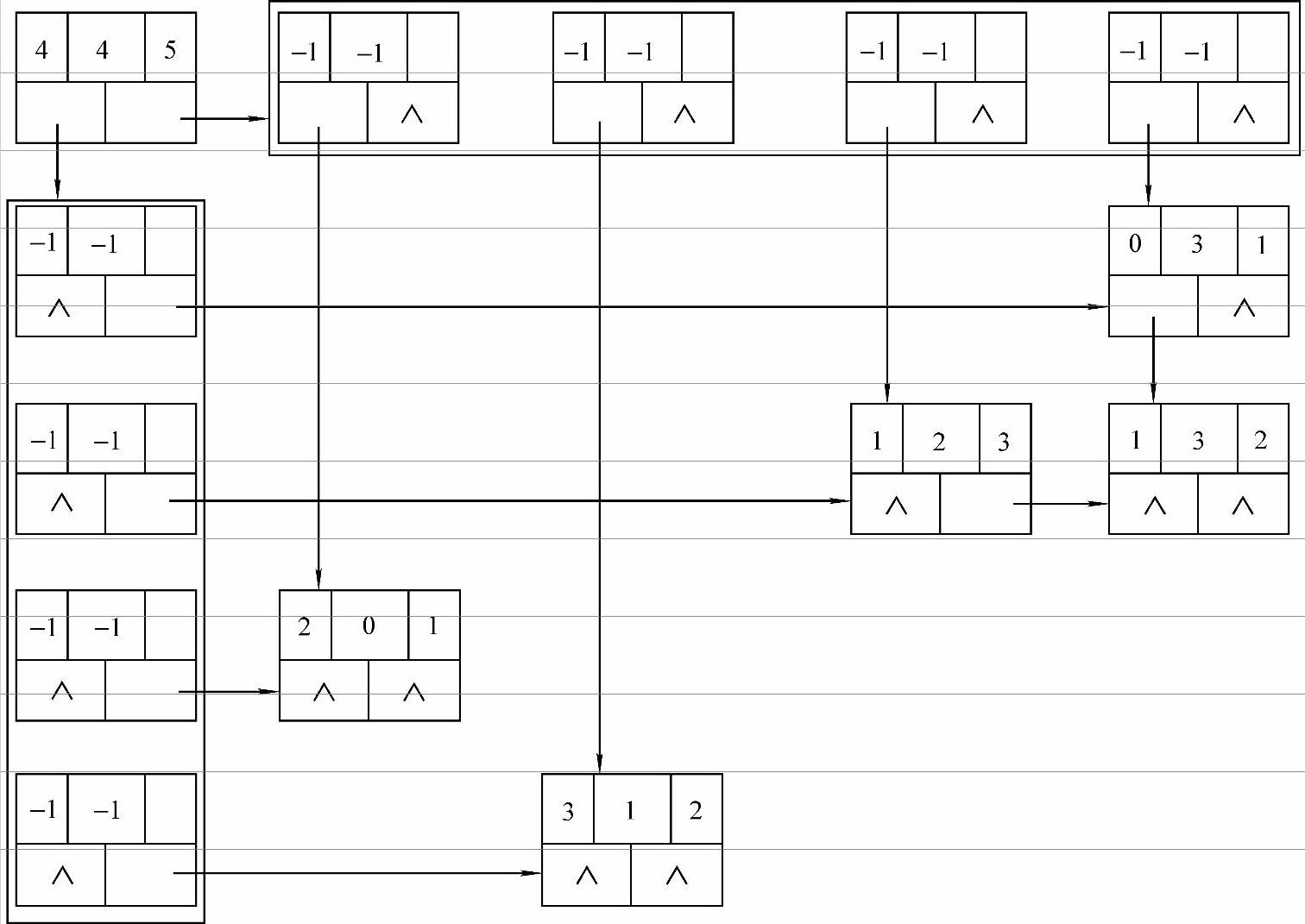
图5-6 稀疏矩阵的十字链表表示

由图5-6可知，十字链表中的两种结点的结构定义如下：

1）普通结点结构定义。

2）头结点结构定义。

【例5-5】 给定一个稀疏矩阵A，其尺寸为m×n，非零元素个数为k，建立其对应的十字链表存储结构。

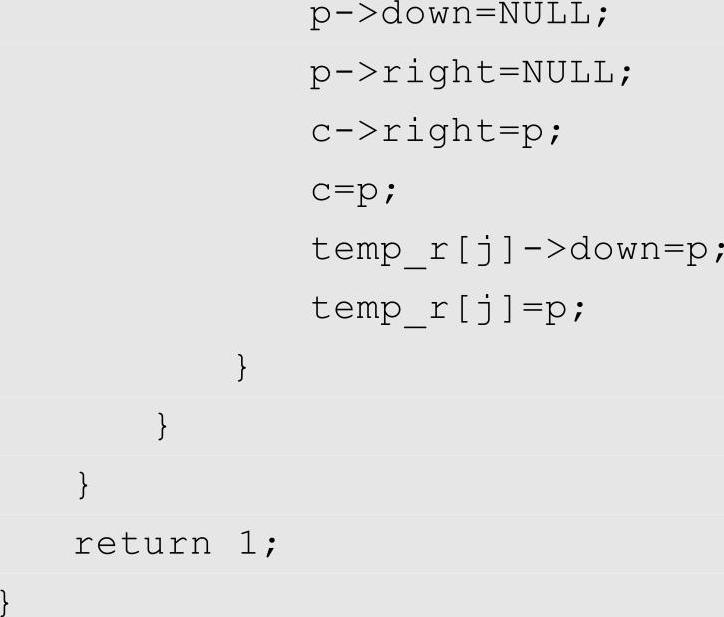
本题较为简单，只需逐行扫描矩阵A，当发现非零元素时，申请结点空间，设置结点值，并将其链入行向和列向的链表中即可，算法实现代码如下：