先看一种特殊情况，见表4-7。当j等于5，发生不匹配时，因next[5]=4，则需将j回朔到4进行比较；又因next[4]=3，则应将j回朔到3进行比较……由此可见，j需要依次在5、4、3、2、1的位置上进行比较，而模式串在1到5的位置上的字符完全相等，因此较为聪明的做法应该是在j等于5处发生不匹配时，直接跳过位置1到4的多余比较，这就是KMP算法改进的切入点。

表4-7 一种特殊情况的next数组

将上述过程推广到一般情况为：

若p_j等于p_k1（k1等于next[j]），则继续比较p_j与p_k2（k2等于next[next[j]]），若仍相等则继续比较下去，直到p_j与p_kn不等（kn等于next[next[…next[j]…]]，嵌套n个next）或kn等于0时，则next[j]重置为kn。一般保持next数组不变，而用名为nextval的数组来保存更新后的next数组，即当p_j与p_kn不等时，nextval[j]赋值为kn。

下面通过一个例题来看一下nextval的推导过程。

【例4-1】求模式串ABABAAB的next数组和nextval数组。

首先求出next数组，见表4-8。

表4-8 例4-1的next数组

1）当j为1时，nextval[1]赋值为0，特殊情况标记。

2）当j为2时，p₂为B，p_k1（k1等于next[2]，值为1）为A，两者不等，因此nextval[2]赋值为k1，值为1。

3）当j为3时，p₃为A，p_k1（k1等于next[3]，值为1）为A，两者相等，因此应先判断k2是否为0，而k2等于next[next[3]]，值为0，所以nextval[3]赋值为k2，值为0。

注意：步骤3）中p₃与p_k1（k1等于next[3]）比较相等后，按照之前的分析应先判断k2是否为0，再让p₃继续与p_k2比较，注意到此时nextval[next[3]]即nextval[1]的值已经存在，故只需直接将nextval[3]直接赋值为nextval[1]即可，即nextval[3]=nextval[1]=0。

推广到一般情况为：当p_j等于p_k1（k1等于next[j]）时，只需让nextval[j]赋值为nextval[next[j]]即可，原因有两点：

①nextval数组是从下标1开始逐渐往后求得的，所以在求nextval[j]时，nextval[next[j]]必已求得。

②nextval[next[j]]为p_j与p_k2到p_kn比较结果的记录，因此无须再重复比较。

4）当j为4时，p₄为B，p_k（k等于next[4]）为B，两者相等，因此nextval[4]赋值为nextval[next[4]]，值为1。

5）当j为5时，p₅为A，p_k（k等于next[5]）为A，两者相等，因此nextval[5]赋值为nextval[next[5]]，值为0。

6）当j为6时，p₆为A，p_k（k等于next[6]）为B，两者不等，因此nextval[6]赋值为next[6]，值为4。(www.daowen.com)

7）当j为7时，p₇为B，p_k（k等于next[7]）为B，两者相等，因此nextval[7]赋值为nextval[next[7]]，值为1。

由此求得的nextval数组见表4-9。

表4-9 例4-1的nextval数组

总结求nextval的一般步骤：

1）当j等于1时，nextval[j]赋值为0，作为特殊标记。

2）当p_j不等于p_k时（k等于next[j]），nextval[j]赋值为k。

3）当p_j等于p_k时（k等于next[j]），nextval[j]赋值为nextval[k]。

观察求next数组的函数getnext（）的核心代码段：

在注释1处next[i]已求出，且next[0…i-1]皆已求出，则结合上边的总结，要求nextval，可以在1处添加如下代码：

显然，在注释2处用next数组来回朔j的代码可以用已求得的nextval数组代替（注意，j往前跳，之前的nextval值已经求得），修改后的代码如下：

j=nextval [j]；//2

通过以上分析，我们完全可以将函数getnext（）中的next数组用nextval数组替换掉，最终得到求nextval的代码：

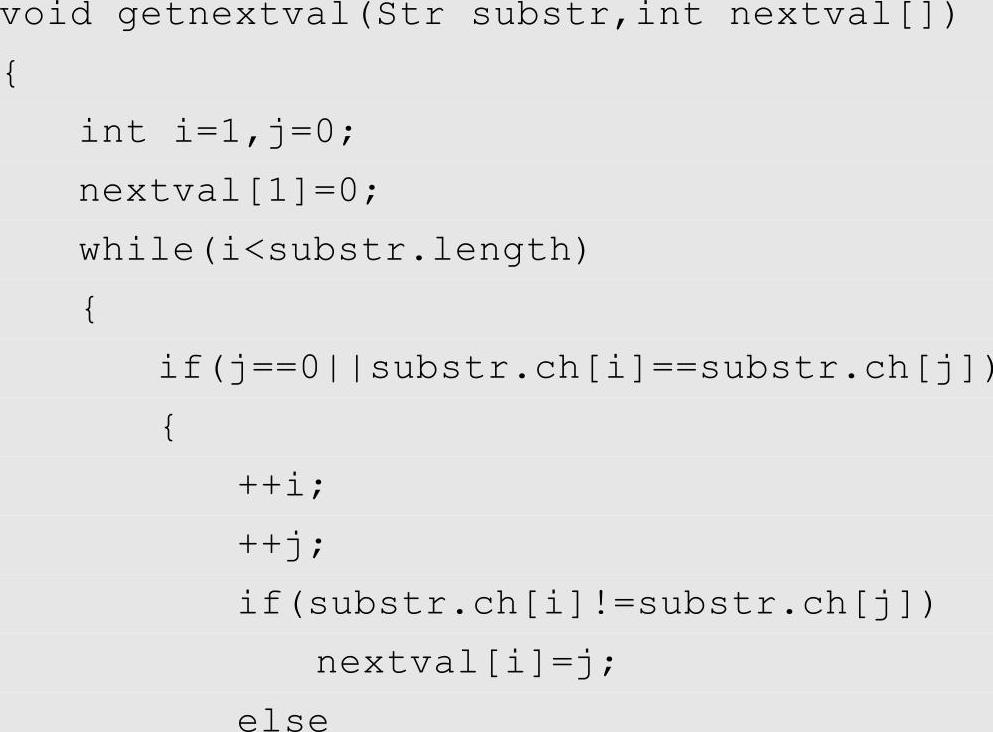
♥感觉KMP算法很难理解？请扫描本书封面二维码，那里有详解视频，可能会对你的理解有帮助。