设主串为s₁s₂…s_n，模式串为p₁p₂…p_m，在上一节的简单模式匹配算法过程中有一个多次出现的关键状态，见表4-2，其中i和j分别为主串和模式串中当前参与比较的两个字符的下标。

表4-2 主串和模式串匹配关键状态

模式串的前部某子串p₁p₂…p_j-1与主串中的一个子串s_i-j+1s_i-j+2…s_i-1匹配，而p_j与s_i不匹配。每当出现这种状态时，简单模式匹配算法的做法是：一律将i赋值为i-j+2，j赋值为1，重新开始比较。这个过程反映到表4-2中可以形象地表示为模式串先向后移动一个位置，然后从第一个字符p₁开始逐个和当前主串中对应的字符做比较；当再次发现不匹配时，重复上述过程。这样做的目的是试图消除s_i处的不匹配，进而开始s_i+1及其以后字符的比较，使得整个过程得以推进下去。

如果在模式串后移的过程中又出现了其前部某子串p₁p₂…与主串中某子串…s_i-2s_i-1相匹配的状态，则认为这是一个进步的状态。因为通过模式串后移排除了一些不可能匹配的状态，来到了一个新的局部匹配状态，并且此时s_i有了和模式串中对应字符匹配的可能性。为了方便表述，记表4-2中描述的状态为S_k，此处的新状态为S_k+1，此时可以将简单模式匹配过程看成一个由S_k向S_k+1推进的过程。当由S_k来到S_k+1时有两种情况可能发生：其一、s_i处的不匹配被解决，从s_i+1继续往下比较，若来到新的不匹配字符位置，则模式串后移寻找状态S_k+2；其二、s_i处的不匹配仍然存在，则模式串继续后移寻找状态S_k+2。如此进行下去，直到得到最终结果。

说明：为了使上边其一与其二的表述看起来清晰工整且抓住重点，此处省略了对匹配成功与失败这两种容易理解的情况的描述。

说明：模式串后移使p₁移动到s_i+1，即模式串整个移过s_i的情况也被认为是s_i处的不匹配被解决。

试想，如果在匹配过程中可以省略掉模式串逐渐后移的过程，而从S_k直接跳到S_k+1，则可以大大提高匹配效率。带着这个想法我们把S_k+1状态添加到表4-2中得到表4-3。

表4-3 匹配关键状态对比

观察表4-3发现，p₁p₂…p_j-1与s_i-j+1s_i-j+2…s_i-1是完全相同的，且我们研究的是如何从S_k跳到S_k+1，因此，表4-3关于主串的那一行完全可以删去，得表4-4。

表4-4 F串前后重合

由表4-4可知，p₁p₂…p_t-1与p_j-t+1p_j-t+2…p_j-1匹配。记p₁p₂…p_j-1为F，记p₁p₂…p_t-1为F_L，记p_j-t+1p_j-t+2…p_j-1为F_R。所以，只需要将F后移到使得FL与FR重合的位置（见表4-4中灰色区域所示）即可实现从S_k直接跳至S_k+1。

总结一般情况：每当发生不匹配时，找出模式串中的不匹配字符p_j，取其之前的子串F=p₁p₂…p_j-1，将模式串后移，使F最先发生前部（F_L）与后部（F_R）相重合的位置（见表4-4中灰色区域所示），即为模式串应后移的目标位置。

本节为了使问题表述得更形象，采用了模式串后移这种分析方式。事实上，在计算机中模式串是不会移动的，因此需要把模式串后移转化为j的变化，模式串后移到某个位置可等效于j重新指向某位置。容易看出，j处发生不匹配时，j重新指向的位置恰好是F串中前后相重合子串的长度+1（串F_L或F_R长度+1）。通常我们定义一个next[j]数组，其中j取1～m，m为模式串长度，表示模式串中第j个字符发生不匹配时，应从next[j]处的字符开始重新与主串比较。

特殊情况：

1）模式串中的第一个字符与主串i位置不匹配，应从下一个位置和模式串第一个字符继续比较。反映在表4-2中即从s_i+1与p₁开始比较。

2）当串F中不存在前后重合的部分时（不可将F自身视为和自身重合），则从主串中发生不匹配的字符与模式串第一个字符开始比较，反映在表4-2中即从s_i与p₁开始比较。

下边以表4-5中的模式串为例，介绍求数组next的方法。

表4-5 一个模式串

(www.daowen.com)

1）当j等于1时发生不匹配，属于特殊情况1），此时将next[1]赋值成0来表示这个特殊情况。

2）当j等于2时发生不匹配，此时F为“A”，属于特殊情况2），即next[2]赋值为1。

3）当j等于3时发生不匹配，此时F为“AB”，属于特殊情况2），即next[3]赋值为1。

4）当j等于4时发生不匹配，此时F为“ABA”，前部子串A与后部子串A重合，长度为1，因此next[4]赋值为2（F_L或F_R长度+1）。

5）当j等于5时发生不匹配，此时F为“ABAB”，前部子串AB与后部子串AB重合，长度为2，因此next[5]赋值为3。

6）当j等于6时发生不匹配，此时F为“ABABA”，前部子串ABA与后部子串ABA最先发生重合，长度为3，因此next[6]赋值为4。

7）当j等于7时发生不匹配，此时F为“ABABAB”，前部子串ABAB与后部子串ABAB最先发生重合，长度为4，因此next[7]赋值为5。

注意：6）和7）中出现了“最先”字眼，以7）为例，F向后移动，会发生两次前部与后部的重合，第一次是ABAB，第二次是AB，显然最先发生重合的是ABAB。之所以选择最先的ABAB，而不是第二次的AB，是因为模式串是不停后移的，选择AB则丢掉了一次解决不匹配的可能性，而选择ABAB，即使当前解决不了，则下一个状态就是AB，不会丢掉任何解决问题的可能。这里也解释了一些参考书中提到的取最长相等前后缀的原因，7）中的ABAB或AB在一些参考书中称之为F的相等前后缀（即F_L和F_R为F的相等前后缀），ABAB是最长相等前后缀，并且很显然的是，越先发生重合的相等前后缀长度越长。

由此得到next数组，见表4-6。

表4-6 next数组

说明：上面1）～7）步骤介绍的求解next数组的方法虽然不是一种高效方法，但是在做选择题时是一种方便的手工求解方法，考生需要熟练掌握。

讲过了如何手工求next数组的方法，下面介绍一种适用于转换成代码的高效的求next数组的方法。以表4-4中的情形为例，next[j]的值已经求得，则next[j+1]的求值可以分两种情况来分析。

1）若p_j等于p_t，显然next[j+1]=t+1，因为t为当前F最长相等前后缀长度（t为F_L和F_R长度）。

2）若p_j不等于p_t，将p_j-t+1p_j-t+2…p_j当作主串，p₁p₂…p_t当作子串，则又回到了由状态Sk找S_k+1的过程，所以只需将t赋值为next[t]，继续进行p_j与p_t的比较，如果满足1）则求得next[j+1]，不满足则重复t赋值为next[t]，并比较p_j与p_t的过程。如果在这个过程中t出现等于0的情况，则应将next[j+1]赋值为1，此处类似于上边讲到的特殊情况2）。

说明：S_k直接跳到S_k+1，也就是通常所说的简单模式匹配算法中i不需要回朔。

注意：KMP算法中的i不需要回朔，这里隐藏着一个考点。i不需要回朔意味着对于规模较大的外存中字符串的匹配操作可以分段进行，先读入内存一部分进行匹配，完成之后即可写回外存，确保在发生不匹配时不需要将之前写回外存的部分再次读入，减少了I/O操作，提高了效率，在回答KMP算法较之于简单模式匹配算法的优势时，不要忘掉这一点。

经过上面的分析可以写出求next数组的算法如下（其中，变量i和j与分析中的i和j无关）：

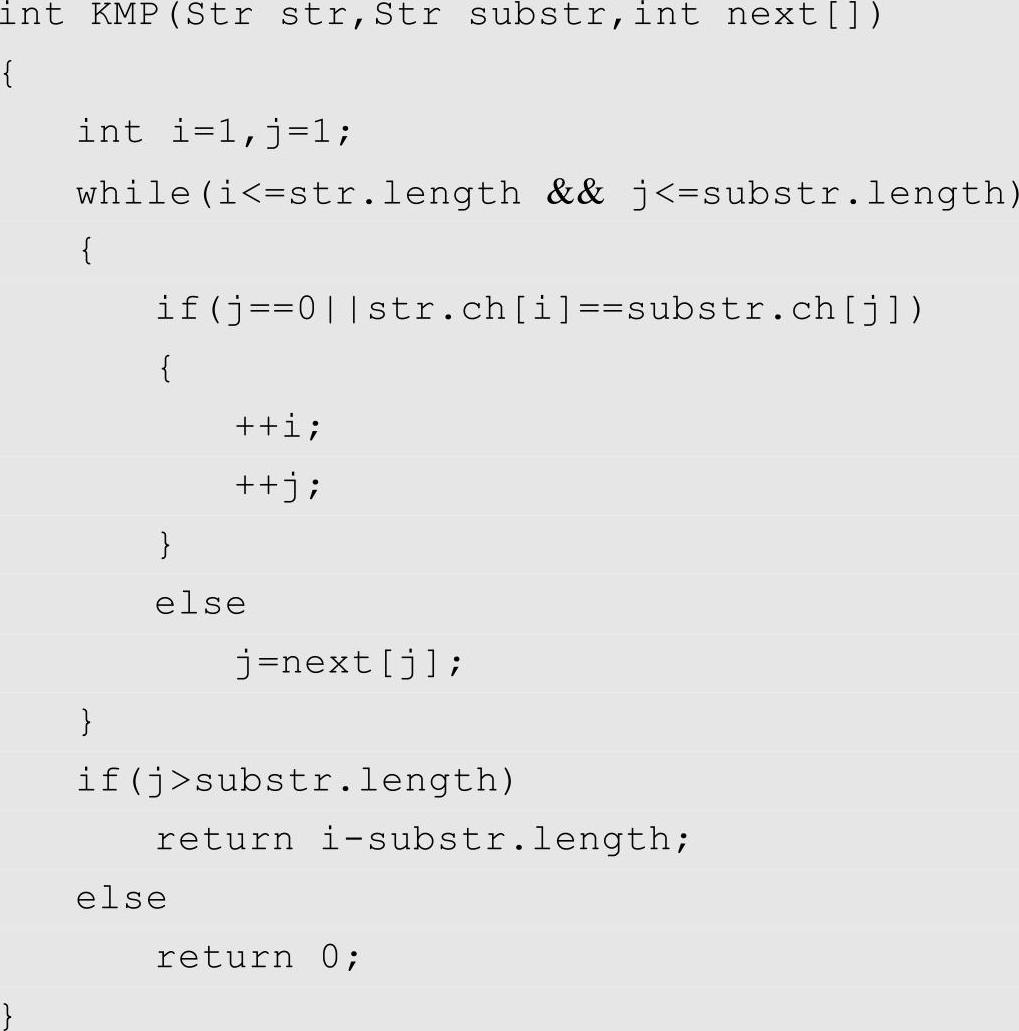
得到next数组之后，将简单模式匹配算法稍作修改就可以得由状态S_k直接跳到S_k+1的改进算法，这就是知名的KMP算法，代码如下：