1.循环队列

在顺序队中，通常让队尾指针rear指向刚进队的元素位置，让队首指针front指向刚出队的元素位置。因此，元素进队的时候，rear要向后移动；元素出队的时候，front也要向后移动。这样经过一系列的出队和进队操作以后，两个指针最终会达到数组末端maxSize-1处。虽然队中已经没有元素，但仍然无法让元素进队，这就是所谓的“假溢出”。要解决这个问题，可以把数组弄成一个环，让rear和front沿着环走，这样就永远不会出现两者来到数组尽头无法继续往下走的情况，这样就产生了循环队列。循环队列是改进的顺序队列。图3-4所示为循环队列元素的进队/出队示意图。

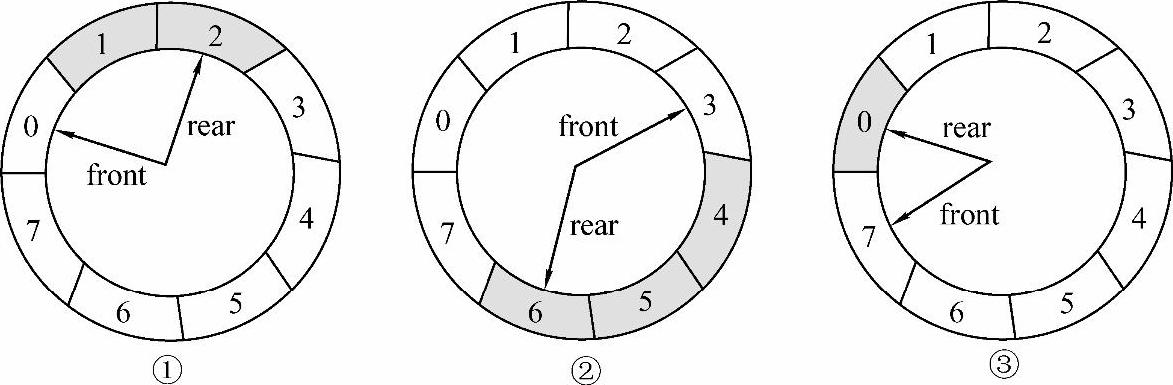
图3-4 循环队列元素的进队/出队示意图

图3-4中进队/出队的变化情况如下：

①由空队进队两个元素，此时front指向0，rear指向2。

②进队4个元素，出队3个元素，此时front指向3，rear指向6。

③进队2个元素，出队4个元素，此时front指向7，rear指向0。

从图3-4中由①到③的变化过程可以看出，经过元素的进进出出，即便是rear和front都到了数组尾端（图3-4中③所示），依然可以让元素继续入队，因为两指针不是沿着数组下标递增地直线行走，而是沿着一个环行走，走到数组尽头的时候自动返回数组的起始位置。

要实现指针在递增的过程中沿着环形道路行走，有一个方法，就图3-4中的例子，拿front指针来说，可以循环执行语句front=（front+1）%8，若front的初值为0，在一个无限循环中，则front的取值为0，1，2，3，4，5，6，7，0，1，2…，即以0～7为周期的无限循环数，也就是front沿着图3-4所示的环在行走。对于一般情况，上述语句可写为front=（front+1）%maxSize（maxSize是数组长度）。图3-5所示为循环队列两个特殊的状态：队满和队空（rear的情况和front类似）。

由图3-5可以看出，循环队列必须损失一个存储空间，如果右图中的空白处也存入元素，则队满的条件也成了front==rear，即和队空条件相同，那么就无法区分队空和队满了。

2.循环队列的要素

通过以上讲述可以总结出循环队列的4个要素。

（1）两个状态

1）队空状态：qu.rear==qu.front。

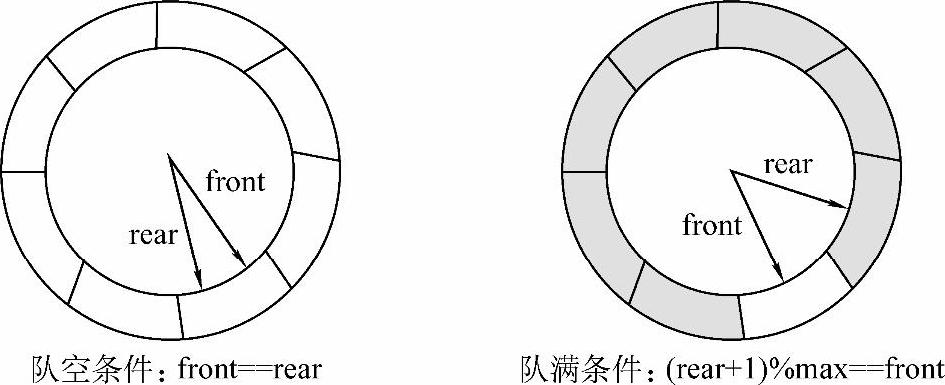
图3-5 循环队列队空与队满的判断

2）队满状态：（qu.rear+1）%maxSize==qu.front。(www.daowen.com)

（2）两个操作

1）元素x进队操作（移动队尾指针）。

qu.rear=（qu.rear+1）%maxSize；qu.data[qu.rear]=x；

2）元素x出队操作（移动队首指针）。

qu.front=（qu.front+1）%maxSize；x=qu.data[qu.front]；

说明：本书中，元素入队时，先移动指针，后存入元素；元素出队时，也是先移动指针再取出元素。其他书上可能有不同的次序，其实本质是一样的，考生只需适应一种写法，对于程序设计题目已经足够。对于选择题，则可根据题目描述来确定是先存取元素，再移动指针，还是采用其他处理顺序。

3.初始化队列算法

4.判断队空

5.进队算法

6.出队算法

说明：这里和前面讲到的情况一样，以上这些函数在书写程序题目的时候并不实用，需要在题目中提取其中有用的操作。