本书中如果没有特殊说明，则链表都是含有头结点的链表。

【例2-3】 A和B是两个单链表（带表头结点），其中元素递增有序。设计一个算法，将A和B归并成一个按元素值非递减有序的链表C，C由A和B中的结点组成。

分析：

已知A、B中的元素递增有序，要使归并后的C中元素依然有序，可以从A、B中挑出最小的元素插入C的尾部，这样当A、B中的所有元素都插入C中时，C^一定是递增有序的。哪一个元素是A、B中最小的元素呢？很明显，由于A、B是递增的，因此A中的最小元素是其开始结点中的元素，B也一样。只需从A、B的开始结点中选出一个较小的来插入C的尾部即可。这里还需注意，A与B中的元素有可能一个已经全部被插入到C中，另一个还没有插完，如A中所有元素已经全部被插入到C中，而B还没有插完，这说明B中的所有元素都大于C中的元素，因此只要将B链接到C的尾部即可。如果A没有插完，则用类似的方法来解决。

经过以上分析可以写出如下代码：

微信答疑

提问：

1）C-＞next=NULL；与r-＞next=NULL；是不是表示到目前（这两句代码结束的地方）为止C链表已经构造完成？

2）为什么LNode*p=A-＞next这行代码可以表示p来跟踪A的最小值结点？A-＞next不是表示取A的下一个分量的意思吗？

3）为什么代码只用了if语句就可把剩余结点接入C的尾部，如果有多个剩余结点，岂不是应该用一个循环来将所有结点逐一接入？

回答：

1）C-＞next=NULL；在这个程序中表示从A链表中取下头结点作为新链表的头，r-＞next=NULL；这一句其实是可以去掉的，因为下边两个if语句必须有一个执行。

2）A-＞next表示A链表的开始结点（头结点后边的那一个），A链表是递增的，用p指向它，即p指向A的最小结点，即用p来跟踪A的最小结点。

3）类比一下现实生活中的接链子，是仅需要接上断掉的一环，还是需要把所有环都断掉重新接一遍？

知识点总结：

例2-3中涵盖了两个知识点：一个是尾插法建立单链表；另一个是单链表的归并操作。上面的程序就是单链表归并操作的标准写法，希望同学们熟练掌握。下面提取出尾插法建立单链表的算法，供参考。

假设有n个元素已经存储在数组a中，用尾插法建立链表C。

以上是尾插法，与尾插法对应的建立链表的算法是头插法，代码如下：

在上述算法中不断地将新结点插入链表的前端，因此新建立的链表中元素的次序和数组a中的元素的次序是相反的。假如这里修改一下例2-3的题干，将归并成一个递增的链表C改为归并成一个递减的链表C，那么如何解决呢？只要将插入过程改成头插法即可解决。这里不需要r追踪C的终端结点，而是用s来接收新的结点，插入链表C的前端。(www.daowen.com)

归并成递减的单链表的算法代码如下：

上述头插法的程序中提到了单链表的结点插入操作，此操作很简单。假设p指向一个结点，要将s所指结点插入p所指结点之后的操作如图2-14所示，其语句如下：

s-＞next=p-＞next；

p-＞next=s；

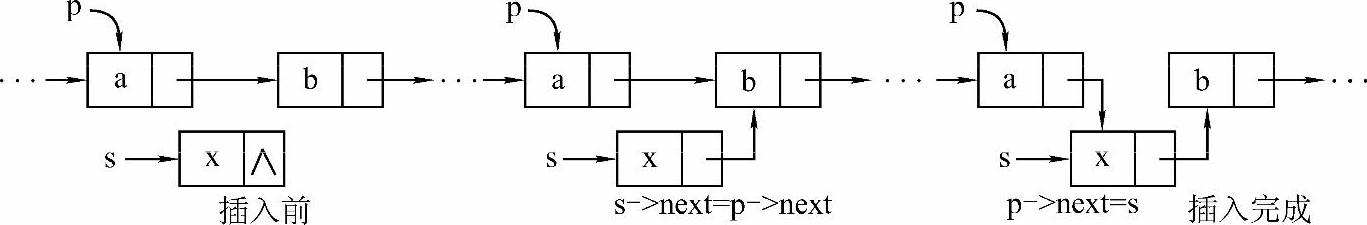
图2-14 插入操作过程

注意：以上插入操作语句能不能颠倒一下顺序，写成p-＞next=s；s-＞next=p-＞next；呢？显然是不可以的，因为第一句p-＞next=s；虽然将s链接在p之后，但是同时也丢失了p直接后继结点的地址（p-＞next指针原本所存储的p直接后继结点的地址在没有被转存到其他地方的情况下被s所覆盖，而正确的写法中，p-＞next中的值在被覆盖前已被转存在了s-＞next中，因而p后继结点的地址依然可以找到），这样链表断成了两截，没有满足将s插入链表的要求。

与插入结点对应的是删除结点，也比较简单，要将单链表的第i个结点删去，必须先在单链表中找到第i-1个结点，再删除其后继结点。如图2-15所示，若要删除结点b，则仅需要修改结点a中的指针域。假设p为指向a的指针，则只需将p的指针域next指向原来p的下一个结点的下一个结点即可，即p-＞next=p-＞next-＞next；

这里还需注意，在考试答卷中，删除操作除了修改指针外，还要释放所删除结点的内存空间，即完整的删除操作应该是：

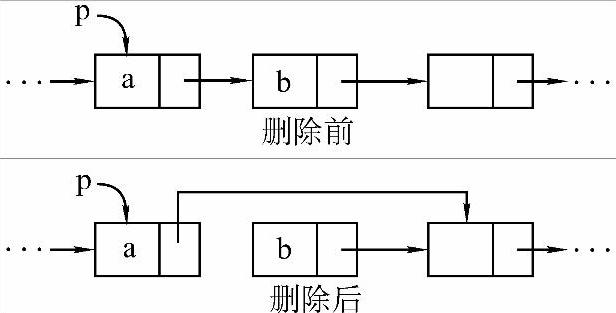
图2-15 删除操作过程

q=p-＞next；

p-＞next=p-＞next-＞next；

free（q）；//调用函数free（）来释放q所指结点的内存空间

掌握了单链表中结点删除的算法后，下边再看一个例题。

【例2-4】 查找链表C（带头结点）中是否存在一个值为x的结点，若存在，则删除该结点并返回1，否则返回0。

分析：

对于本题需要解决两个问题：一个是要找到值为x的结点，另一个是将找到的结点删除。第一个问题引出了本章要讲的单链表中最后一个重要操作——链表中结点的查找。为了实现查找，定义一个结点指针变量p，让它沿着链表一直走到表尾，每遇到一个新结点就检测其值是否为x，是则证明找到，不是则继续检测下一个结点。当找到值为x的结点后就删除该结点。由此可以写出以下代码：

说明：以上程序中之所以要使p指向所要删除结点的前驱结点，而不是直接指向所要删除结点本身，是因为要删除一个结点必须知道其前驱结点的位置，这在之前删除操作的讲解中已经体现。

到此为止，考研中对于顺序表和单链表算法操作部分所涉及的最重要的知识点都已经讲解完。考生务必要熟练掌握这些内容。下面要介绍的是双链表、循环链表以及循环双链表的操作。这些内容考研中虽然也会涉及，但常以选择题的形式出现，重要性也不如以上两部分内容，并且这些内容是在上述两部分内容的基础上稍加变动而来的，比较容易理解。