说明：这一部分先讲例题，然后从例题中总结出考研所需的基本知识点。

【例2-1】 已知一个顺序表L，其中的元素递增有序排列，设计一个算法，插入一个元素x（x为int型）后保持该顺序表仍然递增有序排列（假设插入操作总能成功）。

分析：

由题干可知，解决本题需完成两个操作：

1）找出可以让顺序表保持有序的插入位置。

2）将步骤1）中找出的位置上以及其后的元素往后移动一个位置，然后将x放至腾出的位置上。

其执行过程如图2-12所示。

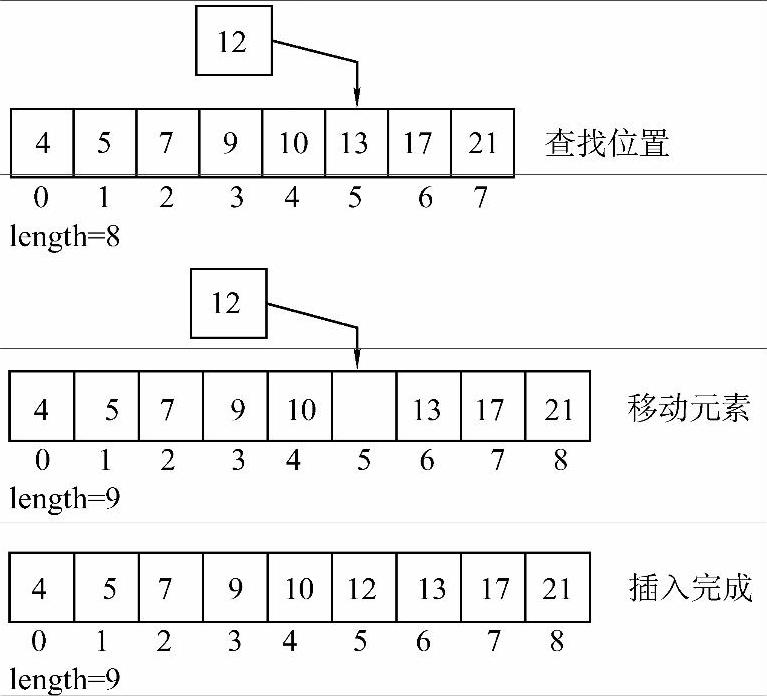
图2-12 元素插入过程

操作一：因为顺序表L中的元素是递增排列的，所以可以从小到大逐个扫描表中元素，当找到第一个比x大的元素时，将x插在这个元素之前即可。如图2-12所示，12为要插入元素，从左往右逐个进行比较，当扫描到13的时候，发现13是第一个比12大的数，因此12应插在13之前。

由此可以写出以下函数，本函数返回第一个比x大的元素的位置。

操作二：找到插入位置之后，将插入位置及其以后的元素向后移动一个元素的位置即可。这里有两种移动方法：一种是先移动最右边的元素，另一种是先移动最左边的元素。哪个才是正确的移动方法呢？答案是先移动最右边的元素。如果先移动最左边的元素，则右边的元素会被左边的元素所覆盖。两种移动方法如图2-13所示。

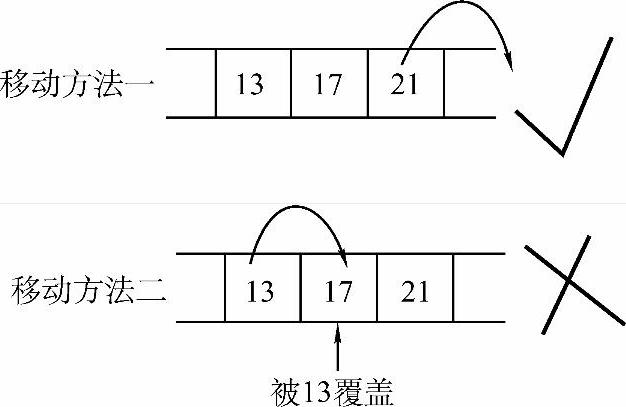
图2-13 两种移动方法

由此可以写出如下代码：

本例题体现了考研中顺序表算法部分要求掌握的以下两个知识点：

（1）按元素值的查找算法

在顺序表中查找第一个值等于e的元素（与上题中查找第一个比x大的元素是同样的道理），并返回其下标，代码如下：(www.daowen.com)

（2）插入数据元素的算法

在顺序表L的第p（0≤p≤length）个位置上插入新的元素e。如果p的输入不正确，则返回0，代表插入失败；如果p的输入正确，则将顺序表第p个元素及以后元素右移一个位置，腾出一个空位置插入新元素，顺序表长度增加1，插入操作成功，返回1。

插入操作代码如下：

【例2-2】 删除顺序表L中下标为p（0≤p≤length-1）的元素，成功返回1，否则返回0，并将被删除元素的值赋给e。

分析：

要删除表中下标为p的元素，只需将其后边的元素逐个往前移动一个位置，将p位置上的元素覆盖掉，就达到了删除的目的。明白了上述元素插入的算法，本算法写起来就相对容易。只需将插入操作中的元素右移改成元素左移即可，插入操作中右移的时候需要从最右边的元素开始移动，这里很自然想到在删除操作中左移的时候需要从最左边的元素开始移动。

由此可以写出以下代码：

说明：通过以上两个例题，可以总结出顺序表的查找、插入和删除三种操作。这是考研中的重点，是考生必须熟练掌握的。

顺序表中还剩下两个比较简单的算法在这里稍做介绍。

（1）初始化顺序表的算法

只需将length设置为0，代码如下：

（2）求指定位置元素的算法

用e返回L中p（0≤p≤length-1）位置上的元素，代码如下：