1.线性表的定义

线性表是具有相同特性数据元素的一个有限序列。该序列中所含元素的个数叫作线性表的长度，用n（n≥0）表示。注意，n可以等于零，表示线性表是一个空表。

线性表是一种简单的数据结构，可以把它想象成一队学生。学生人数对应线性表的长度，学生人数是有限的，这里体现了线性表是一个有限序列；队中所有人的身份都是学生，这里体现了线性表中的数据元素具有相同的特性；线性表可以是有序的，也可以是无序的，如果学生按照身高来排队，矮在前，高在后，则这就体现了线性表的有序性。

2.线性表的逻辑特性

继续拿定义中的例子来进行说明。在一队学生中，只有一个学生在队头，同样只有一个学生在队尾。在队头的学生的前面没有其他学生，在队尾的学生的后边也没有其他学生。除了队头和队尾的学生以外，对于其他的每一个学生，紧挨着站在其前面和后面的学生都只有一个，这是很显然的事情。线性表也是这样，只有一个表头元素，只有一个表尾元素，表头元素没有前驱，表尾元素没有后继，除表头和表尾元素之外，其他元素只有一个直接前驱，也只有一个直接后继。以上就是线性表的逻辑特性。

3.线性表的存储结构

线性表的存储结构有顺序存储结构和链式存储结构两种。前者称为顺序表，后者称为链表。下面通过对比来介绍这两种存储结构。

（1）顺序表

顺序表就是把线性表中的所有元素按照其逻辑顺序，依次存储到从指定的存储位置开始的一块连续的存储空间中。这样，线性表中第一个元素的存储位置就是指定的存储位置，第i+1个元素的存储位置紧接在第i个元素的存储位置的后面。

（2）链表

在链表存储中，每个结点不仅包含所存元素的信息，还包含元素之间逻辑关系的信息，如单链表中前驱结点包含后继结点的地址信息，这样就可以通过前驱结点中的地址信息找到后继结点的位置。

（3）两种存储结构的比较

顺序表就好像图2-1a所示的一排房间，每个房间左边的数字就是该房间离0点的距离，同时也代表了房间号，房间的长度为1。因此，只要知道0点的位置，然后通过房间号就马上可以找到任何一个房间的位置，这就是顺序表的第一个特性——随机访问特性。由图2-1a还可以看出，5个房间所占用的地皮是紧挨着的，即连续地占用了一片空间，并且地皮的块数6是确定的，若在地皮上布置新的房间或者拆掉老的房间（对顺序表的操作过程中），地皮的块数不会增加，也不会减少。这就是顺序表的第二个特性，即顺序表要求占用连续的存储空间。存储分配只能预先进行，一旦分配好了，在对其操作的过程中始终不变。

再看链表，如图2-1b所示，4个房间是散落存在的，每个房间的右边有走向下一个房间的方向指示箭头。因此，如果想访问最后一个房间，就必须从第一个房间开始，依次走过前3个房间才能来到最后一个房间，而不能直接找出最后一个房间的位置，即链表不支持随机访问。通过图2-1b还可以知道，链表中的每一个结点需要划出一部分空间来存储指向下一个结点位置的指针，因此链表中结点的存储空间利用率较顺序表稍低一些。链表中当前结点的位置是由其前驱结点中的地址信息所指示的，而不是由其相对于初始位置的偏移量来确定。因此，链表的结点可以散落在内存中的任意位置，且不需要一次性地划分所有结点所需的空间给链表，而是需要几个结点就临时划分几个。由此可见，链表支持存储空间的动态分配。

图2-1 顺序表和链表的比较

a）顺序表 b）链表

图2-1a所示的顺序表中最右边的一个表结点空间代表没有被利用（顺序表还有剩余空间来注入新数据），如果想在1号房间和2号房间之间插入一个房间，则必须将2号以后的房间都往后移动一个位置（假设房间是可以随意搬动的），即顺序表做插入操作的时候要移动多个元素。而链表就无须这样，如图2-1b所示的链表，如果想在第一个和第二个房间之间插入一个新房间，则只需改动房间后边的方向指示箭头即可，将第一个房间的箭头指向新插入的房间，然后将新插入的房间的箭头指向第二个房间，即在链表中进行插入操作无须移动元素。

链表有以下5种形式（在程序题目中用到的链表结点的C语言描述将在以后的章节中介绍）：

1）单链表。

在每个结点中除了包含数据域外，还包含一个指针域，用以指向其后继结点。图2-2所示为带头结点的单链表。这里要区分一下带头结点的单链表和不带头结点的单链表。

图2-2 带头结点的单链表

①带头结点的单链表中，头指针head指向头结点，头结点的值域不含任何信息，从头结点的后继结点开始存储数据信息。头指针head始终不等于NULL，head-＞next等于NULL的时候，链表为空。

②不带头结点的单链表中的头指针head直接指向开始结点，即图2-2中的结点A1，当head等于NULL的时候，链表为空。

总之，两者最明显的区别是，带头结点的单链表中有一个结点不存储信息（仅存储一些描述链表属性的信息，如表长），只是作为标志，而不带头结点的单链表的所有结点都存储信息。

注意：在题目中要区分头结点和头指针，不论是带头结点的链表还是不带头结点的链表，头指针都指向链表中第一个结点，即图2-2中的head指针；而头结点是带头结点的链表中的第一个结点，只作为链表存在的标志。

2）双链表。

单链表只能由开始结点走到终端结点，而不能由终端结点反向走到开始结点。如果要求输出从终端结点到开始结点的数据序列，则对于单链表来说操作就非常麻烦。为了解决这类问题，构造了双链表。图2-3所示为带头结点的双链表。双链表就是在单链表结点上增添了一个指针域，指向当前结点的前驱。这样就可以方便地由其后继来找到其前驱，从而实现输出终端结点到开始结点的数据序列。

图2-3 双链表

同样，双链表也分为带头结点的双链表和不带头结点的双链表，情况类似于单链表。带头结点的双链表，当head-＞next为NULL时链表为空；不带头结点的双链表，当head为NULL时链表为空。

3）循环单链表。

知道了单链表的结构之后，循环单链表就显得比较简单了，只要将单链表的最后一个指针域（空指针）指向链表中的第一个结点即可（这里之所以说第一个结点而不说是头结点是因为：如果循环单链表是带头结点的，则最后一个结点的指针域要指向头结点；如果循环单链表不带头结点，则最后一个指针域要指向开始结点）。图2-4所示为带头结点的循环单链表。循环单链表可以实现从任一个结点出发访问链表中的任何结点，而单链表从任一结点出发后只能访问这个结点本身及其后边的所有结点。带头结点的循环单链表，当head等于head-＞next时，链表为空；不带头结点的循环单链表，当head等于NULL时，链表为空。

4）循环双链表。

和循环单链表类似，循环双链表的构造源自双链表，即将终端结点的next指针指向链表中的第一个结点，将链表中第一个结点的prior指针指向终端结点，如图2-5所示。循环双链表同样有带头结点和不带头结点之分。当head等于NULL时，不带头结点的循环双链表为空。带头结点的循环双链表中是没有空指针的，其空状态下，head-＞next和head-＞prior必然都等于head。所以判断其是否为空，只需要检查head-＞next和head-＞prior两个指针中的任意一个是否等于head指针即可。因此，以下四句中的任意一句为真，都可以判断循环双链表为空。

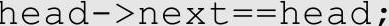
(www.daowen.com)

图2-4 带头结点的循环单链表

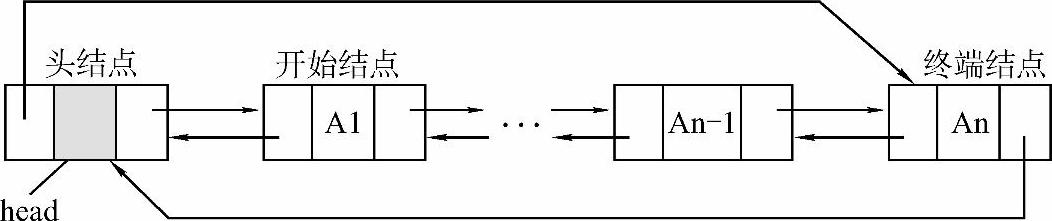
图2-5 循环双链表

上述4种链表可以用4种道路来形象地比喻，如图2-6所示。

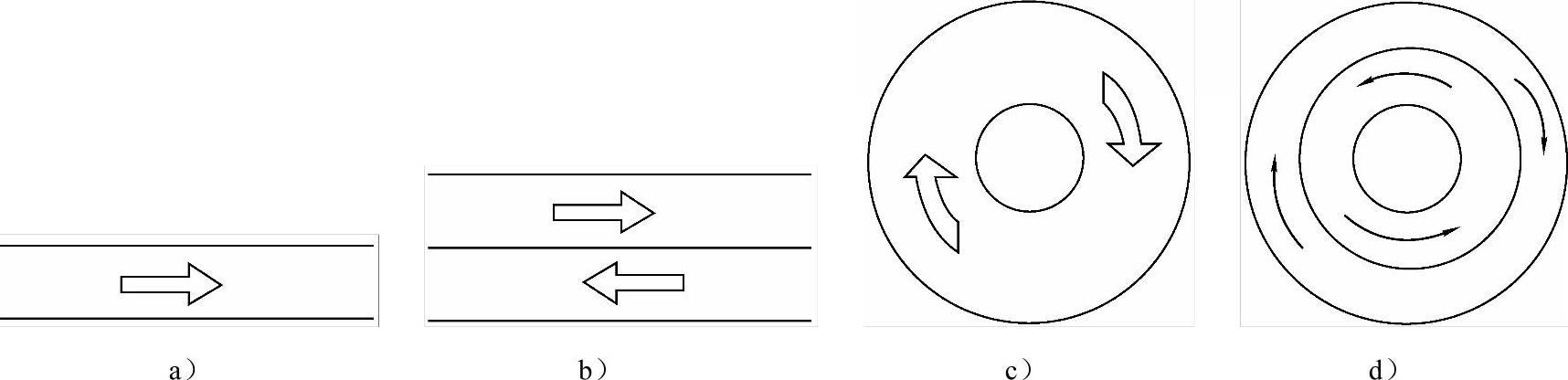
图2-6 链表

a）单链表 b）双链表 c）循环单链表 d）循环双链表

单链表就像图2-6a所示的单行车道，只允许车辆往一个方向行驶；双链表就像图2-6b所示的双向车道，车辆既可以从左往右行驶，也可以从右向左行驶；循环单链表就像图2-6c所示的单向环形车道，车辆可沿着一个方向行驶在这条车道上；循环双链表就像图2-6d所示的双向环形车道，车辆可以沿着两个方向行驶在这条车道上。

5）静态链表。

静态链表借助一维数组来表示，如图2-7所示。

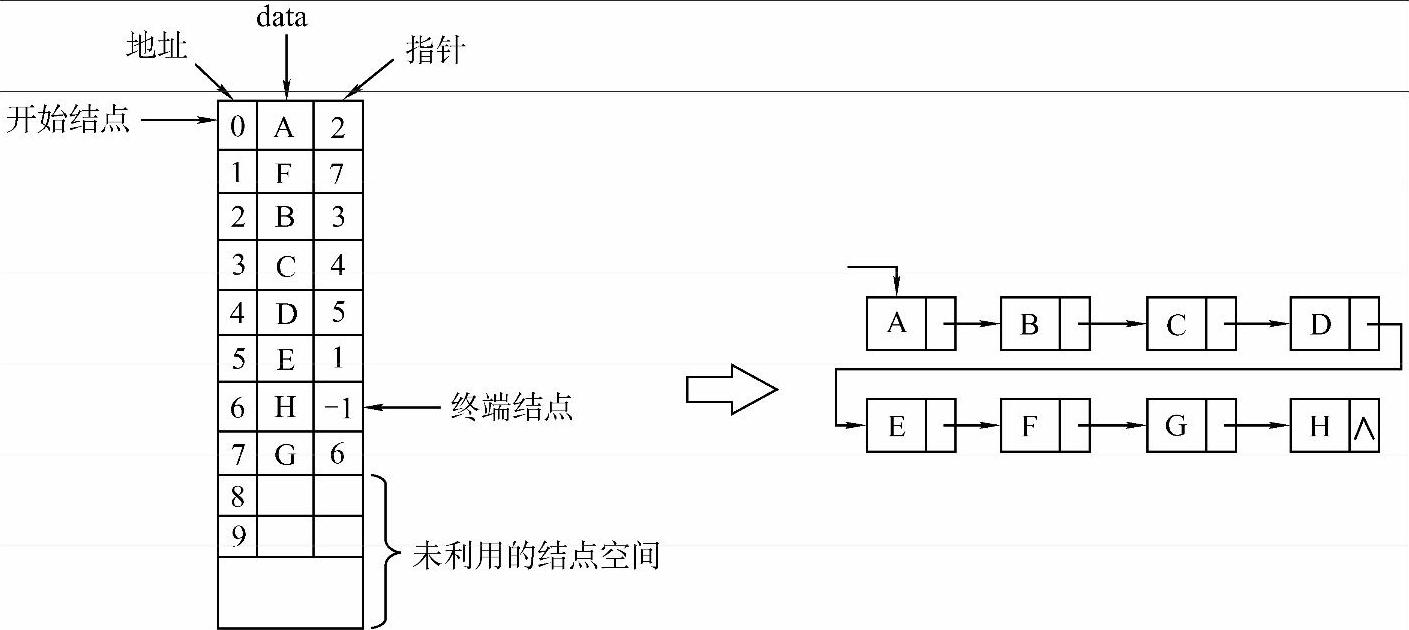
图2-7 静态链表的表示

图2-7中的左图是静态链表，右图是其对应的一般链表。一般链表结点空间来自于整个内存，静态链表则来自于一个结构体数组。数组中的每一个结点含有两个分量：一个是数据元素分量data；另一个是指针分量，指示了当前结点的直接后继结点在数组中的位置（这和一般链表中next指针的地位是同等的）。

注意：静态链表中的指针不是我们通常所说的C语言中用来存储内存地址的指针型变量，而是一个存储数组下标的整型变量，通过它可以找到后继结点在数组中的位置，其功能类似于真实的指针，因此称其为指针。

说明：在考研中经常要考到顺序表和链表的比较，这里给出一个较为全面的答案。

（1）基于空间的比较

1）存储分配的方式：

顺序表的存储空间是一次性分配的，链表的存储空间是多次分配的。

2）存储密度（存储密度=结点值域所占的存储量/结点结构所占的存储总量）：

顺序表的存储密度=1，链表的存储密度＜1（因为结点中有指针域）。

（2）基于时间的比较

1）存取方式：

顺序表可以随机存取，也可以顺序存取（对于顺序表，一般只答随机存取即可）；链表只能顺序存取（所谓顺序存取，以读取为例，要读取某个元素必须遍历其之前的所有元素才能找到它并读取之）。

2）插入/删除时移动元素的个数：

顺序表平均需要移动近一半元素；链表不需要移动元素，只需要修改指针。

对顺序表进行插入和删除算法时间复杂度分析：具有n个元素的顺序表（见图2-8），插入一个元素所进行的平均移动个数为多少（这里假设新元素仅插入在表中每个元素之后）？

图2-8 具有n个元素的顺序表

因为题目要计算平均移动个数，这就是告诉我们要计算移动个数的期望。对于本题要计算期望，就要知道在所有可能的位置插入元素时所对应的元素移动个数以及在每个位置发生插入操作的概率。

①求概率。

因为插入位置的选择是随机的，所以所有位置被插入的可能性都是相同的，有n个可插入位置，所以任何一个位置被插入元素的概率都为p=1/n。

②求对应于每个插入位置需要移动的元素个数。

假设要把新元素插入在表中第i个元素之后，则需要将第i个元素之后的所有元素往后移动一个位置，因此移动元素个数为n-i。

由①和②可知，移动元素个数的期望E为

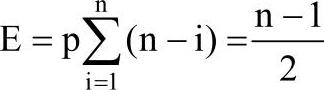
删除操作时，元素平均移动的次数的计算方法与插入操作类似，这里不再讲解。

即要移动近一半元素，由此可以知道，插入和删除算法的平均时间复杂度为O（n）。