（一）基于频次分布法的空间分布型

将柠条豆荚螟幼虫田间调查所得数据以每个样地为1 组，编制实测频次表，计算出每组的平均虫口密度（m）及方差（S2），并进行适合度卡方检验，结果见表2-3。

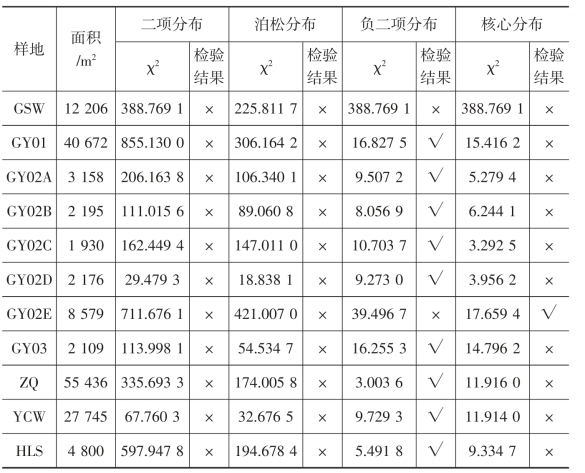
表2-3 豆荚螟在田间的空间分布型拟合表

注：×为不符合该分布，√为符合该分布。

对豆荚螟在11 个样地的空间分布型适合度进行卡方检验，结果显示泊松分布、核心分布、二项分布的适合度χ2 值均远大于相应自由度下时的值，表明豆荚螟幼虫在柠条林间的分布概率小于0.01，即该虫极不适合这3 种分布型。除GSW 样地和GY02E 样地外，其他样地负二项分布的适合度卡方值均小于相应自由度下0.05 水平的卡方值，表明豆荚螟在田间分布属于负二项分布的概率大于0.05，即该虫田间分布特征符合负二项分布型。在GY02E 样地中豆荚螟幼虫符合核心分布，而在GSW 样地中几种分布型都不适合，产生这种现象的原因是不是由抽样误差所致，还有待探讨。总之，豆荚螟在田间的分布型符合负二项分布，基本不受斑块面积大小、斑块隔离程度影响。

（二）基于聚集度指标的空间分布型

采用David 和Moore 聚集度指标I、Beall 扩散系数C、Water 负二项分布参数K、Ca 指标、Lloyd m*/m 指标等聚集度指标测定其空间分布型（表2-4）。

表2-4 豆荚螟种群空间分布型相关指标参数

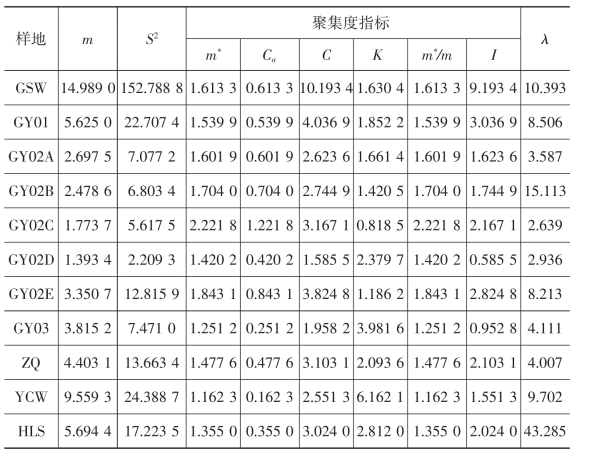
表2-4 的测定结果显示，以平均拥挤度与平均密度的比值（m*/m）作为聚集度指标，在11 个样地中豆荚螟幼虫均呈聚集分布。其他各项指标C＞1，I＞0，K＞0，Ca＞0，m*/m＞1，均符合聚集分布的检验标准，表明豆荚螟幼虫在11 个样地中的空间分布型表现一致，均呈聚集分布格局，不同环境中柠条的生长方式对其空间分布没有影响。

以m*/ S2 指标判断豆荚螟在各样地中的分布型，表2-4 中所有样地中豆荚螟的种群密度m 均大于1，同时m*/ S2 的值均小于1，因此均表现为聚集分布。

（三）空间分布型的回归检验

1.Iwao 的m*-m 回归分析

柠条豆荚螟幼虫的Iwao 线性回归方程为：(www.daowen.com)

m*=0.135 59+1.471 89m（r=0.975 0）

回归方程中α=0.135 59，数值大于0，且β=1.471 89，数值大于1，说明豆荚螟幼虫个体间相互吸引，种群分布的基本成分为个体群，分布表现为聚集分布。对豆荚螟幼虫的回归关系进行方差分析表明，幼虫空间分布的回归关系极显著（F=33.90，P=0.000 3）（图2-4）。

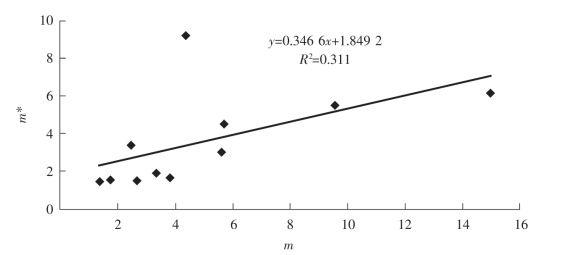
图2-4 豆荚螟幼虫空间分布的Iwao 回归检验

2.Taylor 幂法则

利用Taylor 幂法则，得出豆荚螟幼虫的对数回归方程为：

logS2=0.215 15+1.461 47×logm（r=0.946 8）

方程中loga=0.215 15，数值大于0，b=1.461 47，数值大于1，表明豆荚螟幼虫在所有虫口密度下的空间分布均为聚集分布，并具有密度依赖性，也就是说种群密度越高，分布越聚集。当自由度为9 时，r0.01=0.735，r＞r0.01，线性方程可靠（图2-5）。

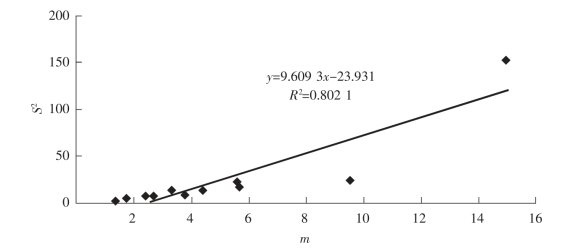
图2-5 豆荚螟幼虫空间分布的Talyor 回归检验

（四）空间分布聚集原因分析

应用Blackith 的种群聚集均数（λ），分析豆荚螟幼虫的聚集原因。将表2-4 各样地的样方平均数（m）与种群聚集均数（λ）进行相关分析，得出：λ=0.191 0m+0.573 8（R=0.265 6）。

由此可知，当柠条豆荚螟幼虫平均密度低于7.467 只/荚时，λ＜2，种群的聚集原因可能是某些环境因素的作用，如气候、土壤条件、植被生长状况等。当柠条豆荚螟幼虫平均密度高于7.467 只/荚时，λ≥2，种群的聚集原因可能是种群自身行为与环境因素综合影响。在11 个样地中λ 均大于2，说明柠条豆荚螟的聚集是由豆荚螟自身的行为习性与环境综合因素造成的。