地统计学最早应用于矿业领域，南非地质学家Krige 在1951年提出了计算矿产储量的方法，即按照样品与待估地段的相对空间位置和相关程度来计算块段品位及储量，并使估计误差最小。此后，法国的Matheron 于1962年提出了区域化变量的概念，产生了地统计学（王正军等，2002）。

自然界种群的空间分布生境，有些是均匀一致的，但大部分是空间异质的，由多个斑块组成。上述对空间格局描述的分布型指数如m*/S2 指标、Taylor 幂法则、Lloyd 的聚集度指标和Iwao 的m*-m 回归指标等，大多数揭示了样本的方差与平均数的关系，都是假定种群生活在均匀的生境之中，强调了样本间的数量变化而忽视了样本的空间位置，从而导致一些令人遗憾的后果：一是这些指数在不同的空间格局中并非不同的，而是都假设任一已知数据独立于整体，并且都有相同的分布，忽略了生态环境之间、生物之间存在的明显相关性；二是对空间格局的分析很大程度上依赖于样本的大小（Liebhold，et al，1993），只注意统计样方的频率分布，不考虑各样方的空间位置，不能反映聚集度在空间的变化（周强等，1998；戈峰，2008）。因此，需要一种能既考虑样本值又考虑样本空间位置及样本间距离的方法来研究种群的空间格局，地统计学就是采用这种方法进行空间分析的工具，它以空间相关为基础，利用分散的数据最大限度地挖掘其中蕴含的空间信息，分析并预测空间相互影响的时序变化及其可能导致的结果，比分布型指数能更直接地描述昆虫种群的空间特征（李友常等，1997；王正军等，2002；Park & John，2004）。将地统计学研究方法引入昆虫生态学领域，来探究昆虫种群的空间格局，目前已成为昆虫空间格局分析的重要方法之一（陈潜等，2018）。

地统计学在昆虫生态学领域的应用主要体现在区域化变量的空间相关性、对调查数据进行空间插值或估值、分析种群动态的时空规律等3 个方面（王正军等，2002）。地统计学研究一般包括2 个步骤：（1）将空间相关性与半变异函数（或称半方差函数）或协方差函数相结合；（2）建立空间插值模型。前期的地统计学侧重于空间格局描述，研究涉及单一种群在同质或异质生境的分布，同一物种成虫、卵、蛹或不同世代在同质生境的分布及多种群的异质空间分布格局。近些年的研究考虑了环境因子对种群分布的作用。

（一）区域化变量

当一个变量在空间上与其位置有关时称为区域化变量，区域化变量在空间上因相互之间的位置关系或空间相关性而存在一定的规律性变化即空间变异。地统计学就是定量地描述并模拟这种空间变异规律的科学，或者说是通过测定区域化变量分隔等距离的样点间的差异来研究区域化变量的空间相关性和空间结构的科学（於崇文，1980；戈峰，2008）。

（二）空间相关性

因空间位置（距离）不同而导致的不同相互作用就是空间相关（spatial correlation），从本质上说，空间相关主要因空间相互作用而产生，而空间相互作用与空间位置信息如空间坐标、空间方向有着密切联系。空间结构（spatial structure）因空间相关而产生，它是区域化变量在空间分布上所呈现出来的结构性和规律性变化。空间相关一般存在2 种情况，即同一空间分布格局内的相关和不同空间分布格局间的相关。同一空间分布格局内的相关就可以用地统计学方法进行研究。

（三）半变异函数

半变异函数是地统计学分析空间相关和空间结构时最常用的工具之一（王正军等，2002）。该函数在区域化变量基础上分析、表现种群在空间上数量的区域化空间变异特征和程度，因此可用区域化变量理论和方法进行研究。

半变异函数是指区域化变量Z（x）和Z（xi+h）的增量平方的数学期望，即区域化变量增量的方差。

对同一个区域内种群的空间格局进行分析时，常用半变异函数来分析样本点的变异空间结构。采用半变异函数分析种群空间格局，实质是观察数据序列Z（xi），i= 1，2，…，n，样本半变异函数值公式为：

式中：γ（h）为半变异函数值，N（h）是被距离h 间隔的数据对（xi，xi+h）的数量，Z（xi）和Z（xi+h）分别是点xi 和点（xi+h）位置处样本的测量值，h 是2 个分隔样点的距离。

计算区域化变量不同方向、不同距离的半变异函数值并应用一定的模型进行模拟，可将这些值及区域模拟值绘制成曲线图，即半变异函数曲线图（图2-1）。它可以直观地分析变量在不同方向的空间变异特征，包括空间分布的结构或空间相关类型、空间变异的范围等。对于一个典型的聚集分布，半变异函数值一般随着距离的增大而增加，亦即区域化变量的空间变异愈来愈大，空间相关性逐渐减小，但增加至某一值时，半变异函数值不再增加而是保持稳定，这表示样点间已不存在空间相关关系。它有3 个特征参数：变程（range）、块金值（nugget）和基台值（sill）。

图2-1 沙冬青种子昆虫密度分布直方图

变程是指区域化变量在空间上具有相关性的范围，也就是半变异函数值不再增加时的距离，反映了区域化变量影响范围的大小。变程也称为空间依赖范围（range of spatial dependence），当变量观测值之间的距离大于独立间距值时，说明它们之间是独立的，若小于独立间距值，则说明它们之间存在着一定的相关关系。因此，在变程之内，数据具有相关性；在变程之外，数据之间互不相关。

基台值是指达到变程后，半变异函数值不再增加，此时半变异函数值就是基台值，代表变量在空间上的总变异大小，反映了变量变化幅度。

块金值就是半变异函数曲线在y 轴上的截距，也称为区域不连续性值。块金值的大小可以反映区域化变量的局部随机性大小，是最小抽样尺度下变量的变异性及测量误差；理论上是h 为0 时的半变异函数值，即γ（0）=0，但γ（0）通常大于0，这可能是由抽样的空间尺度不合适或者数据的内禀随机性引起的（周国法等，1998）。

（四）空间分布特征

计算实验数据的半变异函数值并用合适的曲线（模型）拟合，通过对半变异函数值和模拟曲线形状特征进行分析就可以判断表示昆虫数量特征的变量的空间分布类型，同时揭示样点间空间相关的范围和强弱。

半变异函数常用的几种理论模型有线性模型、高斯模型、指数模型、抛物型模型和球面模型等，都能用来拟合实验半变异函数。线性模型说明研究的种群是随机分布还是均匀分布，即表明数据呈无规律变化，样点间无空间相关性。如果拟合曲线的相关系数较小而方差较大，表明数据呈随机分布；如果相关系数较大而方差较小，则表明数据呈均匀分布。一般而言，球面模型、指数模型、抛物型模型和高斯模型的半变异函数表示的数据是聚集的，模型所对应的空间分布均为聚集分布，但不同的曲线所揭示的空间结构存在很大变异。如球面模型的聚集分布所表明的空间结构是当样点的间隔距离达到变程之前时，样点间的空间依赖性随距离增大而逐渐降低。抛物型模型的聚集分布所表明的空间结构是当样点的间隔距离较小时，样点值有较好的空间连续性（或一致性），即γ（h）较小，而在距离较大时，空间连续性急剧下降，即γ（h）较大。

地统计学中用来拟合实际变异曲线的模型还有球面—球面套合模型、球面—指数套合模型和线性有基台值模型等。(www.daowen.com)

理论模型及公式如下:

1.球面模型

2.指数模型

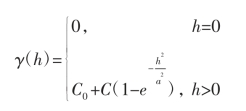
3.高斯模型

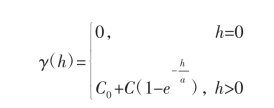
4.球面—指数套合模型

5.球面—球面套合模型

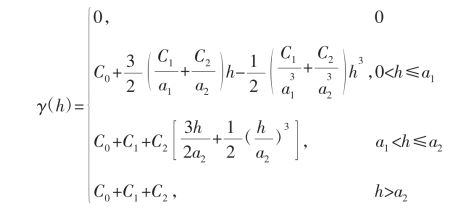
不同理论模型的半变异函数方程中，C0 为块金值，其大小可反映变量的随机程度。C0+C 为基台值，其大小可反映变量变化幅度的大小。

空间变异比［C0/（C0+C）］反映空间变异的随机程度，该比值越大，说明由随机因素引起的空间变异性程度越高，而由空间自相关引起的空间变异性程度越低。一般当该比值小于0.25 时，说明变量具有强烈的空间相关性；比值在0.25～0.75，说明变量具有中等程度的空间相关性；比值大于0.75，说明变量的空间相关性很弱。如果该比值接近1，则说明该变量在整个尺度上具有恒定的变异。

空间结构比［C/（C0+C）或（C-C0）/C］反映了空间结构系数在样点变量差异中所占的比率，依据其大小可判定系统内变量的空间相关程度。小于0.25 则空间相关性较弱，结构性变异较小，随机性变异较大；介于0.25～0.75 之间则有中等程度的空间相关性；大于0.75 则具有较强的空间相关性，结构性变异较大，随机性变异较小。

变程（a）是当半变异函数值达到平衡或最高时的距离，它反映了区域化变量的影响范围或空间依赖性的大小，表示以a 为半径的邻域内的任何其他Z（xi）与Z（xi+h）间存在的空间相关性。

具体选择时主要根据建模误差最小原则：平均预测误差尽可能接近0、均方根误差尽可能小、平均Kriging 标准差尽可能小、无偏估计（平均标准差）尽可能接近0、一致性估计（均方根标准差）接近1、均方根误差与平均Kriging 标准差之间差的绝对值要尽可能小（李哈滨等，1998）。

（五）空间数据插值和空间分布模拟图

Kriging 插值是一种用来估计观测样点间插值的地统计学方法，在已知某变量的半变异函数模拟模型条件下，可以利用样点观测值对研究区域内未取样点x 的区域化变量进行最小误差估值，任意一点Zx 的估计值都可通过该点邻近的n 个有效样本值Z（xi）的线性组合得到：

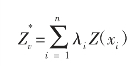
λi 是与样点观测值Z（xi）有关的加权系数，用来表示各样点观测值Z（x）i对估计值的贡献。

用Kriging 插值法的优点是最大限度地利用了空间取样所提供的各种信息。在估计未知样点数值时，它不仅考虑了落在该样点的数据，还考虑了邻近样点的数据，不仅考虑了待估样点与邻近已知样点的空间位置，还考虑了各邻近样点彼此之间的位置关系。除了上述几何因素外，还利用了已有观测值空间分布的结构特征。故这种估计方法比其他传统的估计方法更精确，更符合实际，并且能避免系统误差的出现，给出估计误差和精度。