（一）昆虫种群空间分布型的概念

由于种群栖息地内生物因素（如种内、种间关系）和非生物因素（如地形、地貌、气候、土壤等）间相互作用，种群在一定空间内个体扩散分布有一定的形式，这种形式就是空间分布型（spatial distribution pattern），也称空间分布图式。

不同生物或同一种生物在不同的环境中可形成不同的空间分布型。同种生物在相同的环境条件下，其空间分布型相对稳定。形成各种空间分布型的原因主要有两类，一类是由环境诸如食物分布、气温、湿度等差异引起的，一类是由生物本身的习性如聚集性、竞争行为等因素引起的。

昆虫种类不同，其种群的空间分布型不同，同一种类不同虫期、龄期、密度或环境条件也有差别。研究昆虫种群的空间分布型，不仅有助于确定或改进有效的抽样设计方案，确定昆虫的分布状况，判断昆虫的生活习性，而且可以对研究资料提出适当的数据统计方法。同时，对了解昆虫的发生、扩散和种群管理也有一定的意义。

（二）昆虫种群空间分布型的类型

1.随机分布（random distribution）

个体独立、随机地分配到可利用的单位中去，每个个体占据空间中的任何一点的概率是相等的，并且任何一个个体的存在绝不影响其他个体的分布，即是相互独立的。属于这类分布的可用数理统计上的概率分布模式泊松分布（Poisson distribution）的理论公式拟合。

实际上在野外适合泊松分布的昆虫是很少见的。大多数昆虫的空间分布结构并不随机，且或多或少也有点不均质。

背离随机性有两个不同的方向：一是聚集化，就是在某个单位空间，调查对象任一个体的出现与其他个体的出现有关，即表现为增加了其他个体出现的机会，这样就表现为聚集分布（contagious distribution）。二是均匀化，就是调查对象任一个体出现于某个单位空间，会使别的个体的出现机会降低，个体与个体之间的分布表现为相互之间的离散而形成均匀分布（uniform distribution）。

2.聚集分布

个体不是随机分布的，而是呈疏松的不均匀分布。

（1）核心分布型（core distribution）：这种分布有一个扩散中心，由此中心向周围逐渐扩散，个体形成很多集团或核心，核心之间的关系是随机的，或称奈曼集群分布（Neyman clumped distribution）。例如，昆虫自卵块孵出向四面扩散时的野外空间结构即属于此种分布。

（2）负二项分布型（negative binomial distribution）：个体在田间形成密集度极不均匀的昆虫集团，疏密镶嵌呈嵌纹状，又称嵌纹分布。

属聚集分布的可以用数理统计上的概率分布模式负二项分布、奈曼分布、泊松—二项分布等理论公式拟合，其中适用范围较广的是具有3 个参数的负二项分布公式。

3.均匀分布

均匀分布是指个体呈规则分布，个体间均保持一定的距离，常用二项分布（positive binomial distribution）理论公式拟合。

一般情况下，随机分布在环境条件很一致的情况下出现，而均匀分布则可能出现在个体间竞争激烈的情况下，最为常见的是聚集分布。

要了解种群的特征，尤其是了解准确的密度，就要有适当的抽样技术，就必须测定分布型。

（三）昆虫种群空间分布型的测定方法

昆虫种群空间分布型的研究方法可以归纳为3 类：频次分布拟合χ2检验法、扩散指数法、回归分析法。随着对大量昆虫种群空间格局的实际研究，这些方法得到进一步的改进和发展，常用的测定方法如下（丁岩钦，1980；徐汝梅，1987；马占云，1992；兰星平，1992）。

1.频次分布法

频次分布法是一种经典的方法，用来判断昆虫的空间分布型。首先将田间调查所得数据以每个样地为1 组，编制实测频次表，计算每个样地害虫的平均数（m，即平均密度）、方差（S2）和平均拥挤度（m*）。根据理论频次分布公式求出二项分布、泊松分布、负二项分布和核心分布的理论频次，与各样地实测频次进行比较，经χ2 卡方检验根据吻合程度判断是否符合某种分布型，凡是吻合的（即差异不明显）即可判断为实测组合属于该种分布型。

Lloyd（1969）平均拥挤度公式：m*=m+（S2/m）-1

式中：S2 表示样本方差，m 表示样本平均值。

平均拥挤度表示生物个体在样方中的平均邻居数，它反映了样方内生物个体的拥挤程度。

2.聚集度指标法

根据频次分布表，统计有关统计量。一般采用扩散系数C、丛生指标（聚集度指标）I、Ca 指标、负二项分布参数K、m*/m 指标等聚集度指标测定昆虫种群空间分布型。

（1）Beall 扩散系数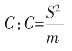

式中：S2 表示样本方差，m 表示样本平均值。

C＜1 为均匀分布；

C=1 为随机分布；

C＞1 为聚集分布。

该指标用于检验种群是否偏离随机分布。C 值多少才不属于随机分布呢？这必须用t 检验来判断，如果差异不显著，属随机分布；如果差异显著，则依差异的正负号而判断为聚集分布还是均匀分布。

（2）David 和Moore（1954）聚集度指标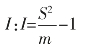

式中：S2 表示样本方差，m 表示样本平均值。

I＜0 为均匀分布；

I=0 为随机分布；

I＞0 为聚集分布。

（3）Kuno（1968）Ca 指标：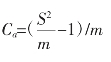

式中：S2表示样本方差，m 表示样本平均值。

Ca＜0 为均匀分布；

Ca=0 为随机分布；

Ca＞0 为聚集分布。(www.daowen.com)

（4）Water 负二项分布参数

式中：S2 表示样本方差，m 表示样本平均值。

K＜0 为均匀分布；

K→+∞为随机分布；

K＞0 为聚集分布。

K 值与虫口密度无关，K 值越小，则表示聚集度愈大。

（5）Lloyd（1967）m*/m 指标：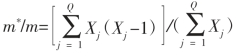

式中：Q 为样方数，Xj 为第j 个样方中的个体数。

m*/m＜1 为均匀分布；

m*/m=1 为随机分布；

m*/m＞1 为聚集分布。

用平均数时受“0”样方的影响很大，在集团很少、“0”样方很多时，虽然平均数m 很小，但是实际上在集团中某些个体间仍极拥挤，种内竞争激烈。因此，平均数难以真正反映生物因素的影响效应。而平均拥挤度不受“0”样方的影响，因为“0”样方没法提供个体的信息。所以，在抽样过程中，有大量“0”样方存在的情况下，平均拥挤度的效果更好，它可以比较真实地反映出种内竞争等生物因素的作用，在生态学研究中具有重要意义。

（6）m*/S2 指标（兰星平，1992）

当种群密度m＜1 时，m*/S2＜1 为均匀分布，m*/S2＝1 为随机分布，m*/S2＞1为聚集分布；

当种群密度m＞1 时，m*/S2＞1 为均匀分布，m*/S2＝1 为随机分布，m*/S2＜1为聚集分布；

当种群密度m=1 时，m*/S2 恒等于1，根据S2 来判断分布型，S2＜1 为均匀分布，S2＝1 为随机分布，S2＞1 为聚集分布。

3.回归分析法

应用Taylor 幂法则和m*-m 回归分析法进一步分析分布格局的内部结构。

（1）Taylor（1961）幂法则：logS2＝loga+blogm

式中：S2 表示样本方差，m 表示样本平均值，a、b 为常数，b 表示种群聚集对密度依赖性的一个测度。

当loga=0，b=1 时，S2=m，种群为随机分布；

当loga＞0，b=1 时，S2/m=a，种群为聚集分布，但不依赖于密度；

当loga＞0，b＞1 时，S2/m=amb-1，种群为聚集分布，依赖于密度；

当loga＜0，b＜1 时，种群为均匀分布，种群密度越高越均匀。

（2）Iwao（1968，1971，1976）m*-m回归指标：m*=α+βm

式中：m*为平均拥挤度，m 为平均数，α 为分布基本成分的平均拥挤度，β 为分布基本成分的空间分布型。

当α=0 时，表明分布的基本成分是个体，无拥挤现象；

当α＞0 时，表明样方中不止一个个体，个体之间相互吸引，存在拥挤现象，可解释为个体在基本成分中以个体群的方式存在；

当α＜0 时，表明分布的基本成分是个体，个体间相互排斥；

当β=1 时，为随机分布；

当β＞1 时，为聚集分布；

当β＜1 时，为均匀分布。

α、β 的不同组合可提供种群不同分布型的信息。

当α=0、β=1 时，为随机分布型；

当α＞0、β=1 时，为奈曼A 型、泊松—二项分布型；

当α=0、β＞1 或α＞0、β＞1 时，为负二项分布型。

这三种条件下种群的分布型均为聚集分布型。

4.聚集原因分析

采用Blackith 提出的种群聚集均数λ 分析聚集原因。

Blackith（1961）种群聚集均数

式中：m 为平均密度，K 为负二项分布参数，γ 为自由度等于2K 时的值，即γ 为χ2 值表中自由度等于2K 与概率（P=0.05）对应的卡方值，可以查表得到。

当λ＜2 时，表明昆虫聚集主要由环境因素引起；当λ≥2 时，表明昆虫聚集由昆虫本身的聚集行为引起，或由昆虫本身的聚集行为与环境的差异性因素共同引起。