6.3.2.1　问题描述

加工系统有M台设备和X种产品，每种产品由所有同一类型的工件组成，所有工件均按照相同的工艺路径加工，每道工序可以在多台不同设备上加工，加工时间随设备性能的不同而变化。同一设备上加工两个不同批次时需要一定的换批时间，换批时间和批次的加工顺序相关。

本案例的调度模型给出如下假设：①在零时刻所有工件均可被加工；②任一工件只有在前一道工序完成后方能进入下一道工序；③工件的工序加工时间和加工设备相关；④不同批次的换批时间与批次的加工顺序相关，设备的调整时间和工件的搬运时间被考虑到换批时间中；⑤每台设备任意时刻最多只能加工一个工件；⑥属于不同批次工件的工序之间没有先后约束；⑦属于同一批次的工件一旦进行加工就不能中断，设备必须加工完该批次的全部工件后，才能加工另一批次。

6.3.2.2　数学模型

为描述方便，下面给出模型中用到的数学符号的意义：

Jx表示第x种产品（x＝1，2，…，X），X为产品类型总数；

Jx，p表示Jx的第p道工序（p＝1，2，…，P），P为总工序数；

Jx，p，k表示Jx，p的第k个工件（k＝1，2，…，sum（Jx）），sum（Jx）为Jx的工件数；

Mx，p表示可以加工Jx，p的设备总数；

Mp，m表示制造系统中第p道工序的第m台设备（m＝1，2，…，Mp），Mp为第p道工序的所有可用设备；

Lx，p，n表示Jx，p的第n个批次（n＝1，2，…，Nx），其中Nx为第x种工件划分的批次总数；

W（Lx，p，n，Mp，m）表示0-1变量，1表示Lx，p，n在Mp，m上加工；

Sum（Lx，p，n）表示Lx，p，n包含的工件数量；

ST（Lx，p，n）表示Lx，p，n的加工开始时间；

FT（Lx，p，n）表示Lx，p，n的加工完成时间；

PT（Lx，p，n）表示Lx，p，n的加工时间；

TUxp，m表示Jx的单个工件在设备Mp，m上的加工时间；

Set x1，x2表示从Jx1切换到Jx2的加工准备时间，若x2为起始工件，则x1＝0且Set0，x2＝0；

M表示批次间的偏序关系，如果在制造系统上的加工顺序先于且没有其他批次加工，则有

目标函数：

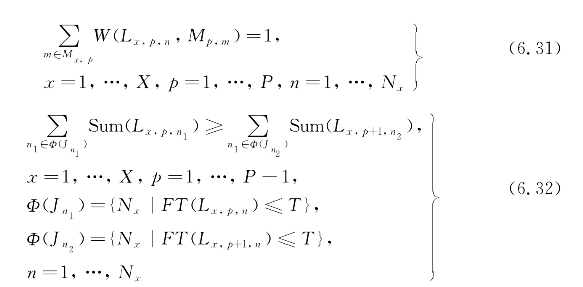
上几式中，式（6.26）表示调度目标为最小化最大完工时间；式（6.27）表示加工数量约束，即对每种产品进行分批，各批次包含的工件的数量之和等于产品包含的工件数量；式（6.28）表示批次的加工时间等于单个工件的加工时间和批次包含的工件数量之积；式（6.29）表示批次的完成时间等于批次的换批时间、加工时间和开始加工时间之和；式（6.30）表示批次的开始加工时间不早于同一设备上的前一批次和同一批次的前道工序完成时间的最大值；式（6.31）表示设备占用约束，即同一批次的所有工件只能在同一台设备上加工；式（6.32）表示批次约束关系，若某时刻Jx，p的所有完成批次数量和为Q，则Jx，p＋1在该时刻所有完成批次的数量和应不大于Q。

6.3.2.3　分批策略

在车间的分批调度问题中，批量大小和生产周期存在U型关系，批量过大或过小都不利于提高车间的运行效率。当批量过小时，批次的数量增加，问题的搜索空间也会相应增大，影响搜索结果，且批次数量的增大会导致换批频繁；当批量过大时，较大的批量占有当前设备，会使后续设备处于闲置等待状态。

适当的批量分割方法能在不明显影响搜索效率的情况下有效减少设备的空闲等待时间，提高生产效率，缩短周期。本案例借鉴批量大小动态结合的思想，提出一种柔性批量分割方法。批量分割时，将同一产品根据其包含的工件数量划分为多个任务，每个任务包含若干个工件，以每个任务作为一个子批量。在排序过程中，把相邻的属于同一产品的任务合并为一个批次。例如：三类产品A，B，C，每类产品各含20个工件，假定以5个工件为一个任务，属于各产品的任务分别记为A，B和C，若初始排序为BBAABBCAACCC，其批次数量为12，经过动态结合后的排序为B2A2B2CA2C3，批次数量为6。

6.3.2.4　混合流水车间分批调度的蚁群算法

蚁群算法模拟蚁群寻找通往食物源最短路径的信息交换机制，被广泛用来解决组合优化问题。图6.12所示为本案例的调度过程图，参照分层法将分批调度过程分为产品分批、设备指派和批次排序三个阶段，并设计蚁群算法进行优化。算法采用三层嵌套结构运行：第一级（产品分批层）蚁群算法为产生分批方案的分批算法，第二级（设备指派层）和第三级（批次排序层）蚁群算法组成混合流水车间调度算法，它以分批的结果为调度对象，通过两层嵌套的形式搜索当前分批结果的最优排序方案。

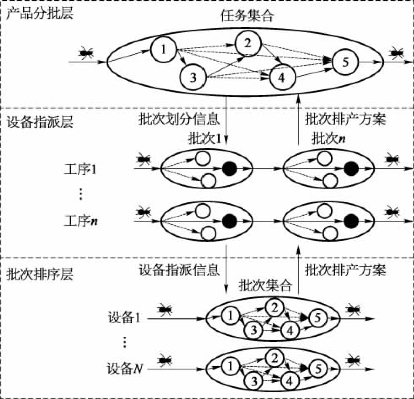
图6.12　调度过程图

假设有两种产品，每种产品包含4个工件且需要经历2道加工工序，每道加工工序有2台设备可以加工，记为｛1，2，3，4｝。选定2个工件为一个任务，则所有产品可分为4个任务，分别为｛11，12，21，22｝，其中“12”表示产品1的第2个任务。若经过产品分批层蚁群算法搜索到的序列为｛11，21，22，12｝，合并“21”和“22”得到的分批方案为，其中表示产品2的第1个批次，工件数量为4；设备指派层蚁群算法以分批结果为输入，搜索批次的设备指派方案，若搜索得到三个批次的设备指派序列为｛1，2，1；3，4，4｝（左边表示工序1的设备指派方案，右边表示工序2的设备指派方案），则可以确定各设备的加工批次为；批次排序层蚁群算法以各设备的加工批次结果为输入搜索设备上的批次排序方案，若搜索到的批次排序序列为｛2，1；1；1；1，2｝（用分号区分不同设备的批次排序方案），则可以确定各设备的批次加工方案为，其排产甘特图如图6.13所示。

1）算法过程

算法运行前设定的参数包括：蚁群算法中的蚂蚁数Qa1，Qa2和Qa3；信息素挥发系数ρ1，ρ2和ρ3；循环计数器q，蚂蚁个数计数器r1，r2和r3，循环次数Q；最优路径等。之后进入如下步骤。

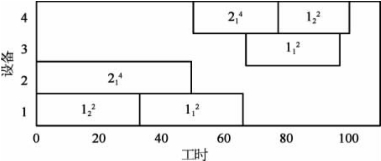
图6.13　蚁群算法排产甘特图(www.daowen.com)

步骤1：生成初始任务序列。

根据产品Jx（x＝1，2，…，X）中任务包含的工件数将其划分为若干任务Ri（i＝1，2，…，N），生成一只蚂蚁a1，并随机选定一个任务（如Ri）作为首个游历的节点。设已游历任务计数器s1＝1，蚂蚁a1的第s1步可以游历的任务集合为Wa1（s1）＝｛R1，R2，…，RN｝－tabua1（s1），其中tabua1（s1）表示蚂蚁a1第s1步已游历的工件集合。蚂蚁a1在第s1步根据状态转移规则从Wa1（s1）中选取节点，并使s1＝s1＋1。重复节点选取过程直到s1＝N，即蚂蚁遍历所有任务节点，得到任务序列。设蚂蚁个数计数器r1＝r1＋1。

步骤2：生成批次序列并对批次进行调度。

批次序列的生产过程参考分批策略，批次调度分为设备指派和批次排序两个阶段，过程如下：

步骤2.1　指派初始工序设备。初始化各设备的可用能力Ck（k＝1，…，M），为工序p（p＝1，…，P）生成一只蚂蚁a2（p）。设已游历批次计数器s2＝0，蚂蚁第s2步从设备集合为Mx，p中选取设备，并使s2＝s2＋1，更新设备能力信息Ck＝Ck－PT（Lx，p，n），Lx，p，n表示第s2步对应的批次节点，W（Lx，p，n，Mp，k）＝1。重复设备选取过程直到s2＝∑Lx，p，n，即蚂蚁遍历所有批次节点，得到最终的设备指派方案。设蚂蚁个数计数器r2＝r2＋1。

步骤2.2　对各设备进行批次排序。根据步骤2.1的设备指派方案，统计各设备需要加工的批次。批次排序过程如下：

步骤2.2.1　生成设备的初始批次序列。初始化工序计数器p（令p＝1），为设备集Mp中每一台设备m生成一只蚂蚁a3（m），并根据设备m上批次转移规则确定批次序列（过程参考步骤1）。

步骤2.2.2　序列解码，得到蚂蚁a3（m）游历所得序列的调度结果。解码过程如下：

（1）若为初始工序（p＝1），则初始化Cmax3，令Cmax3＝0，否则转（2）。

（2）从设备集Mp中取出设备k，由式（6.28）～式（6.30）计算设备k上所有批次（Lx，p，n∈｛W（Lx，p，n，Mp，k）＝1｝）的加工开始时间ST（Lx，p，n）和加工完成时间FT（Lx，p，n），更新设备集Mp＝Mp＼k。

（3）若Cmax3＜FT（Lx，p，n），则更新Cmax3，即Cmax3＝FT（Lx，p，n），转（4），否则直接转（4）。

（4）若Mp＝Φ，则转入步骤2.2.3，否则返回（2）。

步骤2.2.3　判断p＜P是否成立，成立则p＝p＋1，转步骤2.2.1；否则判断r3＜Qa3是否成立，成立则p＝1，转入步骤2.2.1，否则转下一步。

步骤2.2.4　若连续5次搜索结果无变化，则转步骤2.2.3；否则转下一步。

步骤2.2.5　更新蚁群算法的信息素浓度。若，则，更新最优调度方案。信息素更新的方法为：首先对信息素作挥发处理，公式为τn，i（q＋1）＝ρ·τn，i（q）。再对本次循环中取得最短完工时间的那只蚂蚁游历的路径增加信息素，公式为τn，ia3（min）＝τn，ia3（min）＋Δτn，ibest，其中a3（min）为取得最短路径的蚂蚁，。转步骤2.2.1。

步骤2.3　获取搜索到的调度结果。蚂蚁a2（p）搜索到的路径为，并更新调度方案。若r2＜Qa2，则转步骤2.1，否则转下一步。

步骤2.4　若连续5次搜索结果无变化，则转步骤3，否则转下一步。

步骤2.5　更新信息素浓度。若，则，更新最优调度方案。信息素更新的方法参考步骤2.2.5。转步骤2.1。

步骤3：获取搜索到的调度结果。蚂蚁a1搜索到的路径为，并更新调度方案。判断r1＜Qa1是否成立，是则转步骤1，否则转下一步。

步骤4：更新搜索到的局部最优值。若q＞Q，则算法结束，否则转下一步。

步骤5：更新信息素浓度。若，则，更新最优调度方案，信息素更新的方法参考步骤2.2.5。转步骤1。

2）蚁群状态转移规则

在产品分批阶段，蚂蚁在构建解的过程中采用伪随机比例的状态转移规则来选择下一步要加工的任务：q1为初始时刻设定的参数，且0≤q1≤1；q为一个随机数，q∈［0，1］。若q≤q1，则根据选择下一个节点；若q1＞q，则按照式（6.33）计算节点选择概率。

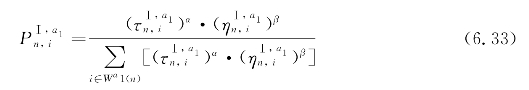
式中　——任务（n，i）间的信息素水平；

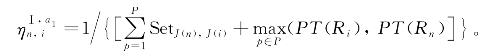
在设备指派阶段，每个蚂蚁a2（p）的状态转移概率为

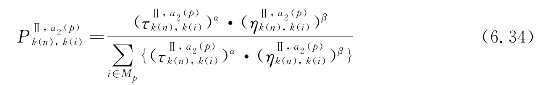
式中　——批次（n，i）所选设备的信息素水平；

，Lx，p，i表示批次节点i。

在批次排序阶段，每个蚂蚁a3（m）的状态转移概率为

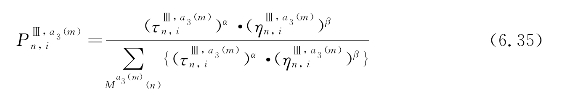
式中　——批次（n，i）间的信息素水平；

，J（n）和J（i）分别表示批n和i的产品种类。