6.2.3.1　数据仿真

对该机场某一天交通需求分布最密集的4个小时的116架到达航班和100架出发航班数据（图6.10）进行分析。在VFR条件下，到达和出发相关时，机场的最大到达容量（主要考虑跑道）为9架次/15 min，最大出发容量为10架次/15 min。如图6.10为其“出发-到达”曲线图。各到达走廊口在各时刻的容量均为10架次/15 min，各出发走廊口在各时刻的容量均为7架次/15 min。在到达和出发不相关的情况下，最大到达容量和最大出发容量均为7架次/15 min，各走廊口的容量不变。

各个时刻的航班数据反映在坐标图上，如图6.10所示，图中的黑点表示“到达-出发”航班数据点。注意到有很多黑点落在了曲线之外。这说明在某一时间段出发成到达的航班需求超过了那一时段机场的出发和到达的容量，造成机场的拥堵和航班的延误。

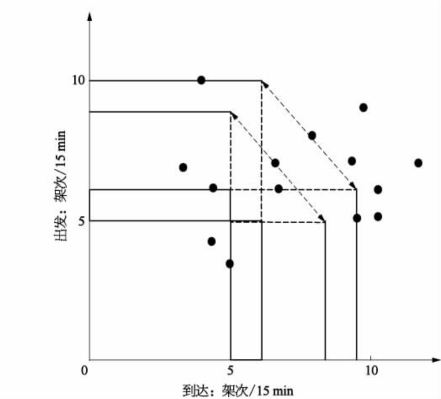
图6.10　航班分布

根据上述Petri网模型对以上航班数据进行分析，在计算时先假定初始时刻各走廊口的等待队列为0。为便于对比，表6.6列出了4种情况下的计算结果，分别是相关容量分配起飞优先表（α＝0.3），相关容量分配着陆起飞同等优先（α＝0.5），相关容量分配着陆优先（α＝0.7）和固定容量分配4种方案。另外在仿真时取Ca/Cg＝20。计算结果见表6.7（以VFR规则为据）。在IFR规则下，机场的容量相对较小一些。如图6.7所示，走廊口的容量基本不变，计算方法同上。这里不再详细列出。

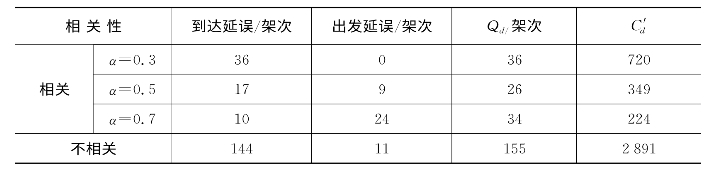
表6.6　模型各方案结果比较

(www.daowen.com)

表6.7　模型仿真结果

6.2.3.2　结果分析

在相同的天气条件下，采用相同的飞行规则时，机场的容量是固定的。但如果分别按到达和出发两过程无关和相关来解决到达航班的流量问题，其延误情况大不相同，如图6.11所示。通过对比可以发现，采用到达和出发相关，动态分配机场容量能够使延误情况得到极大的改善。

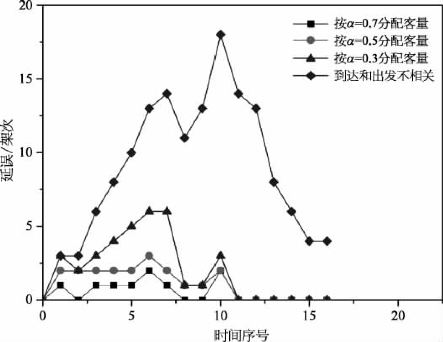
图6.11　总到达航班延误对比

通过表6.6和图6.11的比较结果可以看出，在按相关处理的过程中，决策者可根据参数α的调整来把握整个机场系统总的流量分配。从表6.7到达和出发相关时可以看出，如果α＝0.3，机场总的航班延误架次为36架，惩罚值为720；α＝0.7时，总的延误架次为34架，惩罚值为224；α＝0.5时，总的延误架次最少，为24架，但其惩罚值为349。综合考虑尽量减少航班延误架次及由航班延误造成的损失，就应该选择α＝0.7的分配方案。以上对比分析再次验证了引入抑制弧后的Petri网模型的实效性。