本案例考虑的机场终端区包括机场附近的空中走廊口和跑道系统。在建模过程中,将机场跑道和走廊口两部分看成一个统一的资源系统。通过对跑道和走廊口的容量分析,对通过的航班流量进化控制和优化,达到减少延误、节约成本的目的。
6.2.2.1 机场到达和出发容量
机场的容量主要受跑道容量的限制,但不同的天气条件下机场的容量不尽相同。机场的调度中,在天气情况好、可见度高的情况下,一般采用目视飞行规则(VFR),机场的容量相对较大。在天气较差、能见度低的情况下,采用仪表飞行规则(IFR),机场的容量相对较低。同时机场容量还受滑行道及停机位因素的限制,相对跑道来讲,这些因素影响不大,本案例暂且不考虑这些因素,只简单地把机场容量等同于跑道容量。
每个机场由于其跑道的数目及构型的不同,机场容量也存在差异。根据某机场跑道的构型,得出如图6.7所示容量图。本案例认为机场的到达和出发容量是相互关联的,这种关联关系可用一组“到达-出发”曲线来表示,如图6.7。当机场出现拥挤时,交通管理人员可依据容量曲线来确定其调配方案。
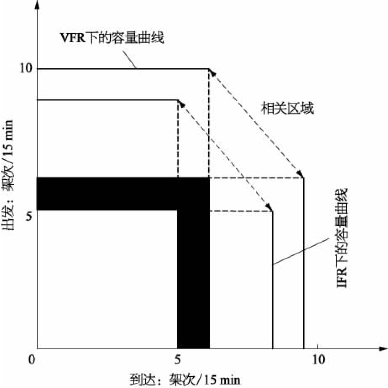
图6.7 不同天气条件下的机场容量曲线
目前也有很多机场空管人员根据具体时段的需求随机改变机场的到达和出发容量,但是大多都是凭直觉决定,可能不是最好的决策。根据存在的曲线关联关系,将可供选择的最佳决策列于表6.4中。
表6.4 分配方案的选择

6.2.2.2 机场终端区的Prtri网模型
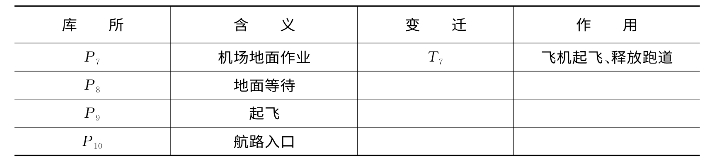
建立的单机场、单跑道机场终端区Petri网模型如图6.8所示,模型中相关的库所及变迁的含义见表6.5。

图6.8 单跑道机场终端区Petri网图模型
图6.8是单跑道机场终端区的扩展Petri网模型,其中P0,P1,P2中的托肯分别表示跑道可用、管制员放行许可、有一架航班请求进入空中走廊入口。P3、P8上的K表示它们最多可容纳的托肯,即出入口走廊的容量。抑制弧上的W表示权值,只有当输入库所中的托宵数小于W时,相应的变迁才能激发。其他没有特别说明的库所则默认其容量为∞。有向弧默认权值为1。
表6.5 图中各符号代表的含义

续 表
该Petri网图模型表示机场终端区各部分的逻辑关系。首先有一架飞机请求进入空中走廊入口,根据变迁使能的条件可知,若变迁T0发生后,P3中的托肯数大于其容量,则变迁不能发生,否则,经过管制许可,航班进入走廊队列P3,某一时段该走廊中的一定数量的航班进入P4等待着陆,抑制弧上的权值表示为该机场的到达容量。当跑道可用时T2激发,P0中的托肯移走,某一时段有不大于机场到达容量的航班可以降落,航班着陆后释放跑道。航班在机场经过停机位分配以及一系列的地面保障作业之后进入P8等待起飞。在该时段能起飞的航班进入P9,当跑道可用,且没有飞机降落,在管制许可下飞机起飞,但实际流量不能超出机场的出发容量。
6.2.2.3 实例分析
为了对某国际机场的航班进离港进行分析,对上述模型做如下改进,各库所及变迁的含义和作用同表6.5。某国际机场有3个出入走廊和2条平行跑道(图中P0用2个托肯表示2条跑道可用)。一般情况下,一条跑道主要用于起飞,另外一条跑道主要用于着陆。但本案例中对两条跑道同等看待,都可同时用于起飞和降落,如图6.9所示。
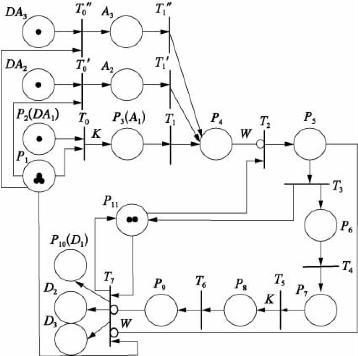
图6.9 某机场终端区Petri网图模型
该模型中增加的几个库所DA1,DA2,DA3分别为请求进入走廊A1,A2,A3的航班队列。Dl,D2,D3分别为出发走廊口。一般机场的调度方式是让飞机在地面等待,对离港航班的控制是只要走廊口仍拥挤,航班暂不起飞,在地面等待,直到满足起飞条件后再起飞,根据需要进入不同的走廊。
1)模型分析
定义一组参数:
T为需要考察的时间,它被分割成长度为15 min的N段不连续时间段I={1,2,…,N},代表一组时间间隔。(https://www.daowen.com)
J={1,2,3}为走廊口集合。
![]() ,i∈I,j∈J,分别表示在第i个时间间隔内第j个到达走廊口的容量、需求、队列和流量。
,i∈I,j∈J,分别表示在第i个时间间隔内第j个到达走廊口的容量、需求、队列和流量。
Carri和Cdepi分别代表在第i个时间间隔内跑道的到达和处罚容量,i∈I。
Qarri,Farri,Qdepi,Fdepi分别代表整个机场系统在第j段时间内的到达和出发过程的队列和流量。
将第I段时间看成一个整体,根据Petri网运行规则,可得到如下公式:
![]() 使能后,在第i段时间,各走廊口的输入为
使能后,在第i段时间,各走廊口的输入为![]() ,输出为
,输出为![]() ,所以在空中走廊的航班数为
,所以在空中走廊的航班数为
![]()
即第i段时间开始走廊口的队列应该是在第i-1段时间开始的走廊口的5L列(原来的标识数)加上前一段时间助初始需求(输入)再减去前一段时间内的实际流量(输出)。
T1,![]() 使能:
使能:

T2使能的条件是
![]()
同理,对于出发的航班有

且从P5到T7的抑制弧表明了到达优先权。
定义一系数α=Farri/(Farri+Fdepi),α表示着陆的优先度,0≤α≤1。
2)目标函数的确立
对一个机场到达和出发过程的控制的最终目的是希望在每段时间内机场的流量都尽可能大,使机场到达和出发的延误航班队列尽可能小。由此构成一个目标函数:

式中 QAi——第i段时间到达的航班数;
QDi——第i段时间出发延误的航班数。
但是现实系统的局限性,使得航班的延误仍会存在,我们的目标还要求一旦出现延误,要尽量使延误造成的损失最小。考虑到航班的空中等待和地面等待给航空公司带来的损失是不一样的,通常认为航班的空中延误造成的单位时间成本损失较大,且存在很大的风险。由于具体的延误成本由很多因素决定,难以给出一个确切的数值,可对到达航班和出发航班的延误人为加上一个不同的惩罚系数Ca和Cg,通常Ca>Cg,由此得到模型的另一个目标函数:

上式两边同除以Cg,得到
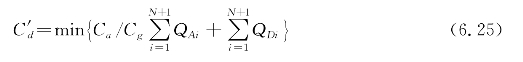
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





