6.1.3.1　模型设置

将从自动化集装箱码头收集到的实验数据存放于data.xlsx中，其中多载AGV的行驶速度AGVSpeed取值5 km/h，作业点个数ODnum取值100。作业点的物理坐标存放于元胞矩阵XY中，运输任务的序号、装载点、交付点和任务大小等数据存放于元胞矩阵ODL中。

为评估算法的性能，用MATLAB编写该遗传算法，并用其求解一系列自动化码头的真实问题，并且在实验中作如下设置：设定小规模问题包含的任务量为1～15，中等规模问题包含的任务量为15～40，大规模问题包含的任务量为40～100。

6.1.3.2　性能指标

实验中共引入两个性能指标：①最优性。小规模问题用MILP算法取出问题最优解的下界，大规模问题通过重复实验求出问题最优解的上下界；②计算时间。现实问题对实时性的要求较高，对计算时间有硬性要求，所以在这里把计算时间作为算法性能的另一指标。

6.1.3.3　实时场景

在本案例算例分析部分共做4组实验，具体场景设置见表6.1，其中：rc为交叉概率；rm为变异概率；ngen为遗传迭代次数。

表6.1　实验场景设置

6.1.3.4　结果分析

1）几组实验

（1）实验1。根据调度模型在MATLAB中编写MILP算法，并用YALMIP工具箱中的GUROBI 6.0求解器求解。容易得出：随着任务量的增大，MILP算法的计算时间呈指数增长趋势，而且当任务量大于8时，短时间内不能求出精确解。用遗传算法再次求解上述各问题，并将两种算法求出的运输时间和所用计算时间记入表6.2。不难发现，两种算法给出的调度方案的运输时间相差不大，但随着问题规模的扩大，遗传算法的计算时间改变很小，但是MILP算法的计算时间却在飞速增长。由于自动化集装箱码头任务量通常较大，且对实时性要求较高，因此，遗传算法更适合用于求解多载AGV调度问题。

表6.2　MILP算法与遗传算法结果对比

（2）实验2。将遗传算法的交叉概率和变异概率分别取0.1，0.2，…，0.9，并将它们一一配对，生成81种不同的组合；分别将这81对交叉概率与变异概率的组合作为遗传算法的交叉概率和变异概率进行运算；为增加可信度，每组实验重复进行5次，取最优结果作为每组实验的结果。令z（i，j）＝100 000/T（i，j），其中T（i，j）为每组实验的实验结果，然后做出如图6.5所示的关于z的等高线示意图。利用遗传算法求出的运输时间越短，越符合码头方面的需要，因此图6.5中的等高线示意图就相当于每对组合的优先性示意图。不难发现，rc＝0.7，rm＝0.3组合和rc＝0.7，rm＝0.5组合的优越性明显高于其他组合，因为变异概率一般较小，所以该遗传算法的最优交叉概率和最优变异概率分别取rc＝0.7，rm＝0.3。

（3）实验3。分别在不同任务量下进行实验，并对比单载AGV与多载AGV完成相应运输任务所需的时间，见图6.6和表6.3。显然，除了任务量为5个的情况，多载AGV都能在更短的时间内完成给定运输任务。(www.daowen.com)

（4）实验4。设定遗传算法的交叉概率与变异概率为最佳组合，即rc＝0.7，rm＝0.3，并且令ngen＝200，然后用一批任务量为50个的运输任务重复实验50次，并分析这50组实验结果。可以得出：用多载AGV完成该批运输任务的最短运输时间为16 502 s，并且遗传算法所给方案的平均误差率为

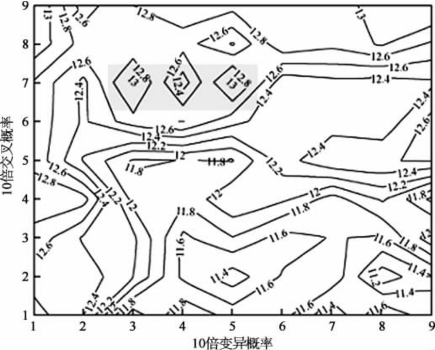
图6.5　交叉概率和变异概率等高线示意图

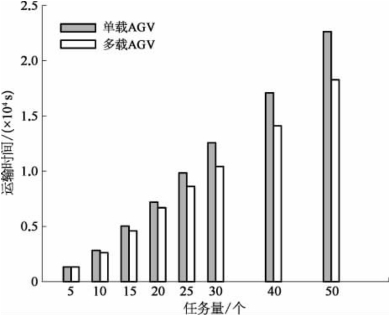
图6.6　单载AGV与多载AGV运输时间对比

表6.3　运输时间对比

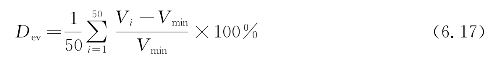
容易得出Dev＝6.21%，显然该误差率相对较小。因此，利用遗传算法求出的多载AGV调度方案值得信赖。

2）实验结论

通过上述4组实验，容易得出如下结论：

（1）该自动化集装箱码头上的多载AGV调度问题是NP难问题。对小规模问题，可以利用YALMIP工具箱中的GUROBI求解器得出精确解，但中大规模问题已经超出精确算法的计算适用范围，只能用遗传算法等智能算法求出近似最优解。

（2）用遗传算法求出的结果与交叉概率和变异概率的赋值有关，如果交叉概率rc和变异概率rm赋值不当，调度结果的可靠性将受到影响。多次重复实验，得出该遗传算法交叉概率与变异概率的最优组合为rc＝0.7，rm＝0.3。

（3）通过实验3中的多载AGV与单载AGV的运输时间对比可以看出，多载AGV的效率更高，更能满足自动化集装箱码头对工作效率的要求，且在码头运作中小箱越多，越能发挥出多载AGV的作用。

（4）重复实验50次，并分析利用遗传算法求出的运输时间和平均误差率，可以得出：对小规模问题，遗传算法可以给出接近于精确解的调度方案，对于中大规模的问题，遗传算法可以给出稳定的近似最优调度方案。