6.1.2.1　符号说明

假设某自动化码头某时刻共有N个运输任务，P表示任务装载点的集合，D表示交付点的集合，I＝P∪D表示装载点与交付点的总集合，并且I＋＝I∪｛S，E｝表示增加了虚拟起点和虚拟终点的任务点集合。运输任务的装载点坐标Pm，交付点坐标Dm和AGV运行速度θ已经给出，并且用Tm，n表示AGV从任务点m到任务点n的运行时间，dm表示AGV在任务点m的容量改变情况，Cm表示在任务点m操作完成后AGV容量的占用情况，C表示AGV的最大负荷能力。

如果AGV相继访问任务点m和n，则决策变量xm，n＝1，否则xm，n＝0；决策变量zm表示AGV在任务点m完成相应操作的时间。

6.1.2.2　调度模型

以最小化最末任务完成时间f为目标，建立自动化集装箱码头多载AGV调度模型，该模型的目标函数与约束条件如下：

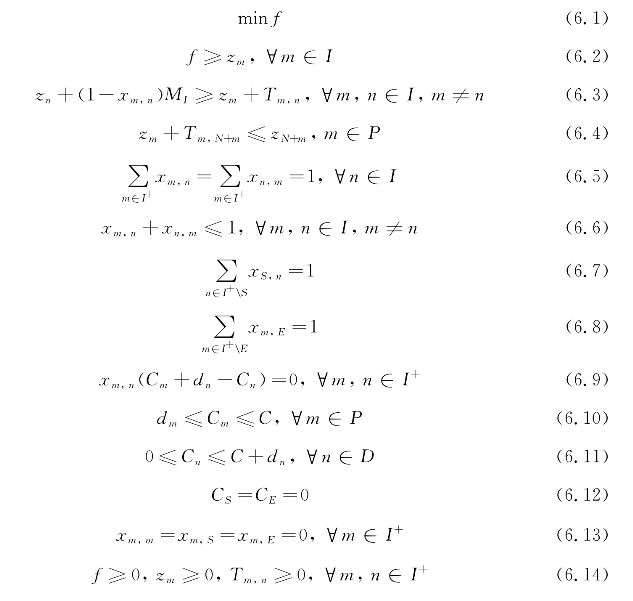
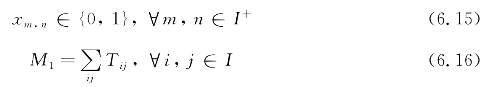
目标函数（6.1）是最小化最末任务完成时间，它服从式（6.2）～式（6.16）的约束。式（6.2）限定最末任务完成时间不小于任何装载和交付操作的完成的时间。式（6.3）～式（6.4）是对操作完成时间的限制：式（6.3）指出，如果xm，n＝1，则zn≥zm＋Tm，n恒成立，其中∀m，n∈I，m≠n；式（6.4）限定任何任务的交付时间一定不小于该任务的装载时间。式（6.5）限定任何运输任务的装载和交付操作一定不是孤立的，即一定有且仅有一个前驱和一个后继。式（6.6）限定任务序中的任何操作能且只能被执行一次。式（6.7）和式（6.8）限定虚拟起点有且仅有一个后继，虚拟终点有且仅有一个前驱。式（6.9）指出，如果AGV在任务点m完成操作后，立即去任务点n执行操作.那么在任务点n完成操作后AGV的负载Cm等于在任务点m完成操作后AGV的负载Cm加上AGV在任务点n的负载变化dn。式（6.10）～式（6.12）是对AGV负载的约束。式（6.13）限定任意任务点m的操作不能作自己的前驱或后继，任何操作不能在虚拟开始前开始，任何任务不能在虚拟结束后开始。式（6.14）给出最小化最终完成时间f，任意操作的完成时间zm和从任务点m到任务点n的时间间隔Tm，n的下界。式（6.15）限定决策变量xm，n为0-1变量。式（6.16）给出了无穷大量M1的取值。

6.1.2.3　遗传算法

VRP问题是数学上的组合优化问题，Golden等证明了该问题是NP难问题，随着问题规模的扩大，计算复杂度将呈指数增长，因此不妨用遗传算法来求解VRP问题的近似最优解。

1）编码与解码

采用集装箱运输任务的序号进行染色体编码，用i表示第i个运输任务，则染色体序列可以表示为｛1，2，3，…，N｝，其中N是运输任务的数量，而且这些运输任务中既有小箱也有大箱。随机生成n个染色体的全排列，就构成了初始种群。图6.2就是一条长度为16的染色体。

图6.2　染色体编码示意图

为清晰形象地表示解码的过程，给出解码示意目，如图6.3所示。图中Ci，j表示从任务i的装载点到任务j的装载点的最短运行时间，于是可以用从虚拟起点到虚拟终点的最短距离表示整个任务序列的最早完成时间。(www.daowen.com)

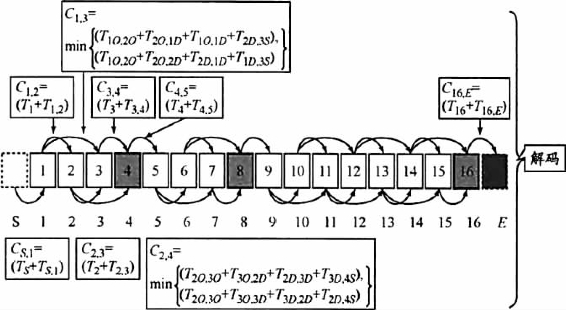
图6.3　解码示意图

2）交叉

本案例采用1990年Syswerda提出的基于位置的交叉方法，这种交叉方法尤其适用于排列形式的染色体，具体过程如下。

输入：两个父代染色体P1，P2。

输出：子代染色体child。

第1步：从父代染色体P1中随机选择一些位置。

第2步：通过复制P1所选位置的基因生成一个子代染色体原型。

第3步：删除染色体P2上选定位置的基因（剩下的部分就是子代染色体child需要的）。

第4步：将P2上的基因从左到右依次放入子代染色体child未确定基因的位置上，这就成功地生成一个子代染色体。

3）变异

本案例中的变异方法采取倒置变异，也就是在染色体上随机选择两个位置，然后颠倒两个位置间的基因序列，如图6.4所示。

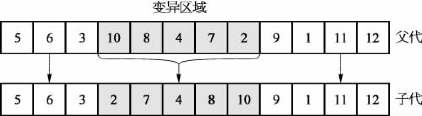
图6.4　倒置变异示意图