以扩展能源中心测试系统作为研究对象，说明多能源系统调度模型及求解算法的合理性。本案例的算例及算法采用MATLAB 2014a和Gams联合编程，即用MATLAB编写知识迁移Q学习算法，用Gams编写机组有功功率确定后的多能源系统优化模型内点法求解，并在CPU为Intel-i7-6700、主频3.4 GHz、内存为8 GB的计算机上运行。

5.5.3.1　仿真模型

能源中心测试系统包括14个节点电力网络、20个节点天然气网络和11个能源中心，能源中心为如图5.24所示的典型能源中心。为说明模型及算法的通用性，本案例对能源中心测试系统进行扩展，如图5.25所示，各子区域之间通过联络线相连，各子区域负荷及机组位置存在差异，其余拓扑及参数相同。其中，区域Ⅰ发电机节点编号为1，2，14；区域Ⅱ发电机节点编号为1，5，15；区域Ⅲ发电机节点编号为2，5，9，13。以下文中所涉及的参数如无特殊说明，均为标值。

多能源系统中，功率基准值为1 MVA，机组都为燃煤机组，有功出力上、下限分别为6 MW和1.5 MW，无功出力上、下限分别为5 MVar和－5 MVar，节点功率因数都为0.9，节点电压上、下限分别为1.1和0.9，同步调相机吸收和发出无功功率，其上下限分别为6 MVar和－6 MVar。天然气输气管道传输系数都为5，加压站特性常数都为0.1，各节点气压上、下限分别为15和10。为了说明综合考虑供能成本和碳排放目标调度的优势，本案例研究三种调度模式：模式1为只以供能成本为目标进行调度；模式2为只以碳排放为目标进行调度；模式3为综合考虑供能成本和碳排放目标进行调度。

5.5.3.2　仿真分析

首先以不同的样本负荷作为预学习样本，获得各调度时段下不同样本负荷的最优Q值矩阵，其次以任务负荷曲线作为目标任务进行多能源系统联合优化调度。知识迁移Q学习算法的参数设置如下：智能体个数为14，学习因子α初始为0.25，折扣因子σ设为0.1，样本学习迭代次数为400，任务优化迭代次数为50。

用知识迁移Q学习算法对多能源系统优化后各模式下天然气发电量占总发电量的比例如图5.26所示。可以看到：若只考虑供能成本，在用电低谷期，几乎没有天然气用于发电，而在用电高峰期，天然气发电比例约占总发电量的18%，在一定程度上起到了发电调峰和联合供热作用，减小了供能成本，但总体来说，由于天然气发电经济效益不明显，天然气发电比例还较少；若只考虑碳排放，由于天然气发电碳排放效益明显，增加天然气发电比例可以明显减少CO2的排放量，因此燃煤机组几乎处于最小发电状态；当综合考虑供能成本和碳排放目标后，天然气发电比例处于模式1和模式2之间，以牺牲一定的供能成本和碳排放来达到两者的最优状态。

为说明多能源系统联合优化的优越性，假设各能源中心天然气只用来供气和供热，发电比例为零，即各能源网络分别单独优化调度时得到各模式下所有调度时段的优化目标结果，及考虑天然气联合供电后求得各模式下的供能成本及碳排放总和见表5.10。

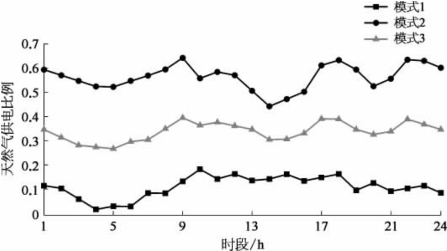
图5.26　天然气发电比例(www.daowen.com)

表5.10　单独优化和联合优化目标总和

由表5.10中数据可知，在各个模式下，多能源系统联合调度优化目标值都比单独优化时小，可见多能源系统优化调度较之于各能源网络单独优化调度的优越性。当单独考虑一个目标时，联合调度优化每个优化时段目标值都比单独优化时好，由于天然气发电经济效益不明显，因此模式1下联合优化的供能成本比单独优化下降1.73%，而得益于天然气的低碳排放；模式2下联合优化的供能成本比单独优化时下降比例达到14.12%。而综合考虑多个目标时，模式3优化结果显示在个别时段，联合优化后的供能成本较单独优化时有所上升，这是因为天然气发电并无明显经济优势，当综合考虑供能成本和碳排放时，模式3是以最大化最小隶属度作为目标，因此系统会牺牲一定的供能成本来降低碳排放，从而导致其供能成本只能下降0.75%，但碳排放下降比例依然明显，达到11.11%。不管以哪种方式，联合优化都能大大降低碳排放，提高系统的环境效益，可见将碳排放纳入优化目标意义重大。图5.27为10台发电机的ΔQ曲线，其中ΔQ＝｜Q（k）－Q（k－1）｜。为方便说明算法的收敛性，同时在图5.27展示了模式3下算法在第11时段的收敛过程。由于模式3目标是使最小隶属度最大，因此其优化曲线呈上升趋势。

从图5.27中可看出：①初始化Q矩阵后，算法一开始便可获得0.544 6的优化结果，这说明采用知识迁移方法获得初始Q矩阵后，算法便开始在较好的动作空间内搜索；②知识迁移后，算法的收敛速度大为提升，算法在38个周期内便可收敛，耗时为289 s，说明知识迁移后，算法收敛快，可满足系统的计算要求。为验证本算法对于多能源优化调度的适用性，本案例引入MAGA以及粒子群优化（PSO）算法与内点法构成级联式算法与本案例知识迁移Q学习进行比较。为体现公平性，每个算法各运行10次。其中MAGA和PSO种群数为100，迭代周期个数为50，MAGA交叉概率取0.8，变异概率取0.9。PSO学习因子取1.5和1，惯性权重取0.5。模式3下各算法在第11时段优化结果见表5.11。

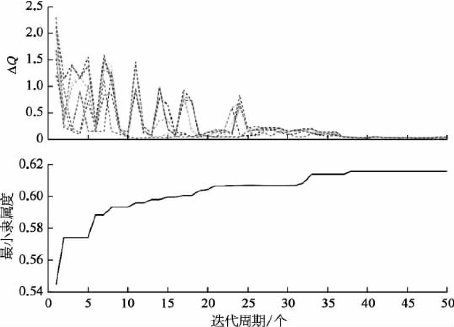
图5.27　目标值收敛曲线

表5.11　模式3下第11时段各算法优化结果

从表5.11中数据可知，对于这种目标函数不连续可微、非凸的非线性规划问题，以人工智能＋内点法的级联式算法都能取得较好的解，三者优化目标值λavr（0＜λavr＜1）相差在2.32%之间，其中MAGA算法效果最好，知识迁移Q学习次之，PSO稍差。由于每次迭代都需进行内点法计算，因此算法主要消耗时间与内点法调用次数有关，MAGA和PSO为5 000次，知识迁移Q学习为700次，因此知识迁移Q学习运行时间明显少于其他算法。可见知识迁移Q学习由于引进了知识迁移，其在较短的迭代周期内便获得了与其余算法相差不大的优化结果，尽管其优化目标值稍差于MAGA，但综合考量各个指标，其优化效果最让人满意。