5.5.2.1　多能源系统的联合优化调度

目前对多能源系统的研究主要包括规划理论、安全分析与优化运行等几个方面，本案例的研究内容主要侧重于优化运行方面，即在已知多能源系统拓扑结构的前提下，实现系统的联合优化调度。

1）天然气潮流

天然气网络由天然气井或储气装置通过天然气管道向负荷输送能源，天然气管道的气流量主要通过调节不同节点调压阀的压力来控制，本案例的天然气稳态模型建模如下。理想情况下，两个节点之间管道内的流量用下式描述：

式中　fmn——节点m至n管道内的天然气流量；

kmn——天然气输气管道传输系数；

pm，pn——节点m和n的气压。

由于管道内存在摩擦而产生传输损耗，为保证天然气网络传送能源的可靠性，网络中还需装设一定数量的加压站，加压站消耗的能量可直接从天然气管道中提取，对于装设在管道m-n之间的加压站，其耗能为

式中　kcom——加压站特性常数；

fkn——加压站至下游节点的气流量；

pk——加压站出气口气压；

pm——加压站上游节点气压。

与电力系统潮流一样，天然气网络潮流也应满足如下节点方程：

式中　A——天然气网络管道-节点关联矩阵；

U——加压站-节点关联矩阵；

A＋U——天然气网络的支路-节点关联矩阵；

f——支路流量向量；

w——节点静流量；

T——加压站消耗流量与节点的关联矩阵；

τ——加压站消耗流量向量。

2）多能源系统的联合调度优化框架

能源中心抽象为一个集各种能源注入、转换、传输及消费的整体，可用于描述不同类型的实体，如钢铁厂、汽车制造厂等工业设施，机场、高铁站、大型商场等建筑，以及乡村、城镇等小型区域。

在能源中心内部，一组能源通过不同的转换器转化为一组用户需要的能源，注入能源及负荷能源包括电能、天然气及热能等常用能源，能源中心内部转换器包括变压器、燃气轮机、燃气锅炉及热转换器等能源转化装置。能源中心的数学模型为

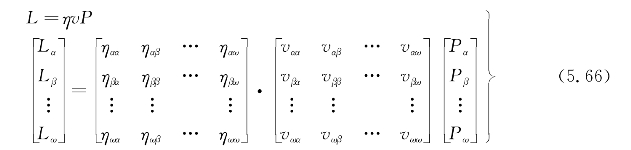
式中　L——负荷向量；

η——效率矩阵；

v——调度系数矩阵，其含义为不同能源通过不同转换器的比例；

P——注入能源向量。

与电力系统优化调度类似，多能源系统的优化调度也是在已知各种能源需求及各种能源网络拓扑结构下，通过调节可控变量，以达到整个系统运行的最优状态，其联合优化调度模型可描述为

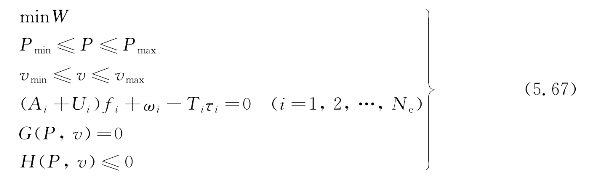
上面各式中，第3个约束条件为第i种能源的节点方程。

式中　W——目标函数；

Pmin，Pmax——能源注入上、下限矩阵；

vmin，vmax——调度系数上、下限矩阵；

Ne——能源种类数；

G——等式约束集；

H——不等式约束集。

3）典型多能源系统的联合调度优化模型

图5.24为一个典型的能源中心，注入能源为电能、天然气，负荷能源包括电能、天然气、热能。变压器、燃气轮机和燃气锅炉一起确定了注入能源和负荷能源之间的转换关系：

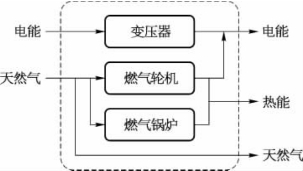
图5.24　典型能源中心

式中　Le——电负荷；

Lh——热负荷；

Lg——天然气负荷；

Pe，Pg——电注入功率和天然气注入功率；

vge，vgh——天然气通过燃气轮机和燃气锅炉的比例；

——变压器效率；

——燃气轮机发电效率；

——燃气轮机热效率；

——燃气锅炉热效率。

典型多能源系统即为多个这样的能源中心连接而成的复杂网络。本案例的多能源系统中，各电源、气源、能源供应网络以及能源中心均服从同一个调度机构进行联合调度，各能源中心预测自身某一时刻的电力、天然气与热力负荷，并将其上报给上层的多能源系统调度机构，多能源系统调度机构对电源、气源、能源中心各能源分配比例等进行统一调度，各环节按此调度结果进行计划运行。

（1）多能源系统调度优化目标。本案例多能源系统单个调度时段的优化目标为供能成本目标We和碳排放目标Wc，为精确计算供能成本，本案例考虑系统的阀点效应：

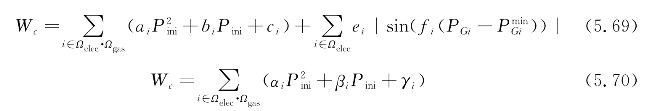
式中　Ωelec——系统注入节点集合；

Ωgas——气源注入节点集合；

Pini——能源注入功率，包括机组注入和气源注入；

PGi，——节点i发电机的有功注入及其下限；(www.daowen.com)

ai，bi，ci——能源成本系数；

ei，fi——系统阀点效应特性参数；

αi，βi，γi——能源碳排放参数。

（2）电力系统约束。本案例电力系统潮流采用交流潮流，原因为：①电力系统潮流与天然气网络潮流是相互影响的，而交流潮流相比于直流潮流有更高的精确性；②电力系统潮流方程只占整个系统潮流方程的少数部分，用直流潮流对计算时间的提升性能不大。电力系统约束包括电力系统潮流约束，发电机有功出力、无功出力上下限约束，节点电压上下限约束和支路容量约束，即

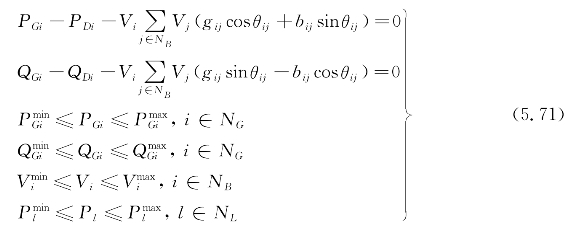
式中　NG，NB，NL——发电机、节点和支路个数；

QGi——节点i发电机的无功注入；

PDi，QDi——节点i的有功负荷和无功负荷；

gij，bij，θij——节点i～j之间的电导、电纳和角度；

Vi——节点i的电压；

Pl——支路l流过的有功功率；

——机组有功出力上限；

——机组无功出力上、下限；

——节点电压上、下限；

——支路容量上、下限。

（3）天然气网络约束。天然气网络约束包括天然气潮流约束、气源注入功率约束、节点气压上下限约束和加压站气压比约束。式（5.63）～式（5.65）中，

式中　NS，NN，NC——气源、节点和加压站个数；

Pgi——节点i气源的注入功率；

pi——节点i的气压；

pk/pm——加压站出气口气压与上游节点气压之比；

——气源功率上、下限；

——节点气压上、下限；

——加压站气压比上、下限。

（4）多目标隶属度转换。对于多目标优化问题，现有算法常以加权的方式转化为单目标求解，或以多目标智能算法进行求解。然而，加权法难以合理地确定各目标的权重值，而多目标智能算法虽然可以求得多目标问题的Pareto前沿，但其耗时较慢，难以满足系统的实时计算要求。为此，本案例采用隶属函数对各目标进行处理。对于以最小为最优的目标W（x），其隶属度可用下式描述：

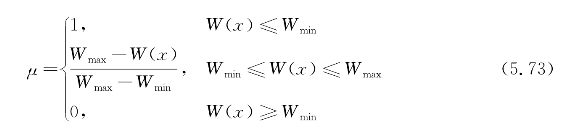
式中　Wmin，Wmax——目标W的最小值和最大值。

本案例供能成本和碳排放最小值为分别单独优化值，最大值为一目标取最小情况下另一目标的取值。

一方面，W（x）的优化值处于Wmin和Wmax之间，另一方面为保证隶属函数连续可微，可用分段函数的中间部分来描述μ与W（x）的关系。根据最大最小满意度原则，将多目标优化问题转化为求解最大最小隶属度的单目标问题，令各目标中最小隶属度为λ，则式（5.68）～式（5.73）中，单目标问题为

此优化模型为不连续可微、非凸的非线性优化模型，整个系统的控制变量主要由三部分构成，电力网络的机组有功和无功功率、节点电压和角度，天然气网络的气源注入、节点压强和管道流量，以及两个网络之间耦合的调度系数与能源中心能源注入。由于系统的成本函数含系统的阀点效应，为不连续可微的非凸函数，用解析法难以求解，而智能算法对这种变量强耦合的复杂系统优化问题求解速度极慢，因此，本案例采用知识迁移Q学习＋内点法的级联式算法求解本模型，即上层Q学习以机组注入有功功率作为动作变量，下层以内点法求解机组注入有功功率确定后的多能源系统优化模型，并通过对历史优化信息的迁移学习加快算法收敛速度。由于每次内点法都将上层Q学习确定的机组注入作为常量，因此下层内点法可直接求解。

5.5.2.2　知识迁移Q学习算法

1）动作空间离散化

传统Q学习只能用于离散变量优化，而本案例模型中机组有功功率为连续值，为了支持Q学习算法能够优化连续变量问题，本案例采用连续变量转化为二进制数的方法将连续的动作空间离散化：

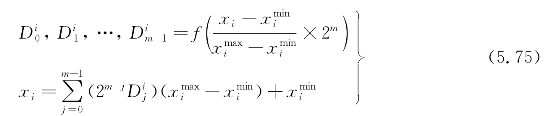
式中　m——变量二进制位数，本案例取20，以保证转化后的连续值能够保留全局信息；

f（x）——将十进制转化为二进制的函数；

xi——解向量X第i个分量；

——变量xi的上、下限；

Dij——变量xi第j个二进制编码。

2）状态-动作矩阵降维

传统的状态-动作QS×A矩阵主要用lookup表来实现。当变量增加时，动作数呈指数增长而导致计算机难以存储。由于每个变量用多个相互关联的二进制编码数表示，前一个二进制编码位的0-1动作选择可作为下一个二进制编码位的状态，因此，可将高维的状态-动作Q转换为多个相互关联的低维状态-动作链。对于每个变量的二进制编码分量Dij分别对应一个Qij矩阵，低维状态-动作链［Qi0，Qi1，…，Qim－1］即构成变量xi的动作选择空间。所有变量的状态-动作链即构成本问题的Q矩阵。

3）Q学习过程

动作空间离散化及状态-动作Q矩阵降维后，Q学习算法的学习过程为：先根据Q矩阵元素大小选择机组注入对应二进制编码的每一位，动作选择只有0-1变量，动作选择完成后经编码转换成连续的机组有功代入多能源系统优化模型，用内点法获得目标值，并将其转化成相应的动作奖励以更新Q矩阵，直到获得最优策略使得奖励回报最大，当多能源系统优化模型收敛到不可行解时，动作奖励为0。

其中，动作选择策略为用轮盘赌的方式在二进制空间中选择：

式中　r——［0，1］之间的随机数；

——基于的概率矩阵中状态为、动作为1的选择概率；

——中状态为s、动作为a的Q值。

状态-动作Q矩阵元素的更新策略为

式中　——在第k步迭代中经a（k）动作后，状态从s（k）转移到状态s（k＋1）的奖励值；

σ——折扣因子；

a（k）——第k步迭代的学习因子，本案例采用基于自然对数衰减的变学习率Q学习，即

式中　T——最大迭代次数。

4）知识迁移

Q学习算法和内点法相结合而成的级联式方法在求解多能源系统的联合优化调度时往往速度较慢，为此，本案例引入知识迁移提高求解速度。算法首先通过对样本的预学习获得不同样本负荷下的最优Q矩阵，然后采用常用的神经网络数据拟合手段得出样本负荷和最优Q矩阵之间的联系。在优化过程中，输入系统的负荷信息至神经网络，便能得到此负荷下的初始Q矩阵，并以此初始Q矩阵为基础用Q学习进行优化。由于系统拓扑不变，负荷又具有相似性，此初始Q矩阵与最优Q矩阵的差异小，因此采用知识迁移可达到加速算法收敛的目的。综上所述，知识迁移Q学习算法与内点法构成级联式算法求解多能源系统联合优化调度模型的流程如图5.25所示。

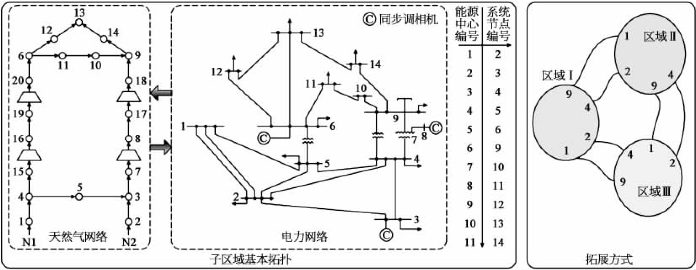
图5.25　扩展能源中心测试系统结构