5.4.2.1　分布式能源系统两阶段调度优化模型

主动配电网下分布式能源系统双层双阶段优化调度就是在主动配电网分层能量管理的基础上，通过电网信息交互和有效传递，分别从日前和实时两个阶段出发，针对全局调度和局部区域调度进行全面协调控制，进而达到分布式能源高效利用的目的，其框架如图5.15所示。一方面，在日前调度优化中，主动配电网以负荷预测以及区域传递信息数据为基础，通过全局优化算法求解出全局区域优化调度控制策略，实现对日前全局信息和实时有效信息的汇集、分配与控制；另一方面，在实时调度中，主要针对当前分布式能源机组的运行状态，对全局调度控制和区域调度情况进行相应的调整，使得分布式能源能够被最大化地消纳和利用。

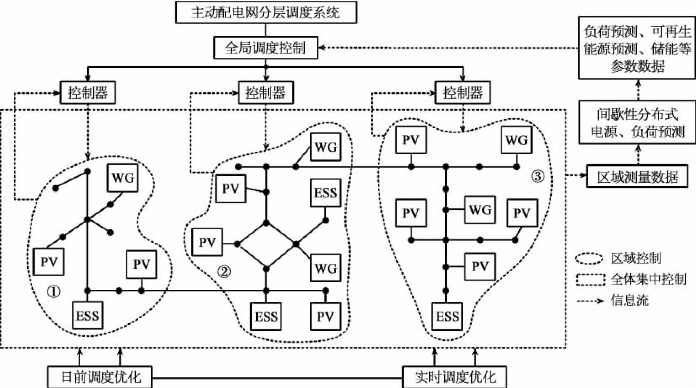
图5.15　主动配电网分层调度系统

1）日前调度优化模型

主动配电网下分布式能源系统调度优化的目的是在确保电网可靠运行和可再生能源最大化利用的前提下，以负荷预测以及间歇式发电出力预测数据为基础，采用最优化算法对主动配电网下的分布式能源（包括分布式电源、储能等）进行统筹协调，确保系统总体运行成本最低，从而实现对分布式能源在周期内的出力情况进行优化调度。在目前电力市场环境条件下，主动配电网下的分布式能源系统日前调度优化的成本主要包括分布式能源发电成本、向主网购电成本、网损成本以及储能成本等。因此，主动配电网下的分布式能源系统的日前调度目标函数可以表示为

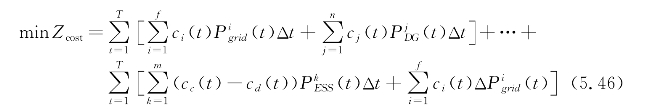
式中　ci（t）——第i条线路在t时刻的电价；

cj（t）——第j台分布式发电单元在t时刻的单位运行成本；

cc（t），cd（t）——储能设备在t时刻的充、放电成本，当设备处于充电状态时，cd（t）的值为0，当设备处于放电状态时，cc（t）的值为0；

f——全部区域内馈线数量；

n——可控分布式发电单元数量；

m——全部储能设备数量；

——第i条线路在t时刻的出口功率值；

——第j台分布式发电单元在t时刻的功率值；

——第k台储能设备在t时刻的充电或放电功率值；

——t时刻的网损值，一般可由式（5.47）求得：

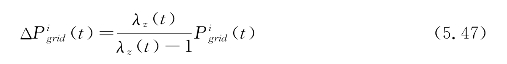
式中　λz（t）——t时刻节点z的综合网损值。

如式（5.46）所示，该目标函数充分考虑了分布式能源以及储能设备合理调度带来的全部成本最小化。当分布式能源的发电利用率较高时，电网输送电能较小，此时说明分布式发电的成本应当小于电网的输电成本；当分布式能源成本高于电网成本时，此时可以购买大量的主网电量来满足当前负荷，另外还可以为储能单元进行充电，从而降低购电成本。

在求解上述目标函数的过程中，全部变量和状态变量必须满足一定的约束条件，本案例求解模型的约束条件表示如下：

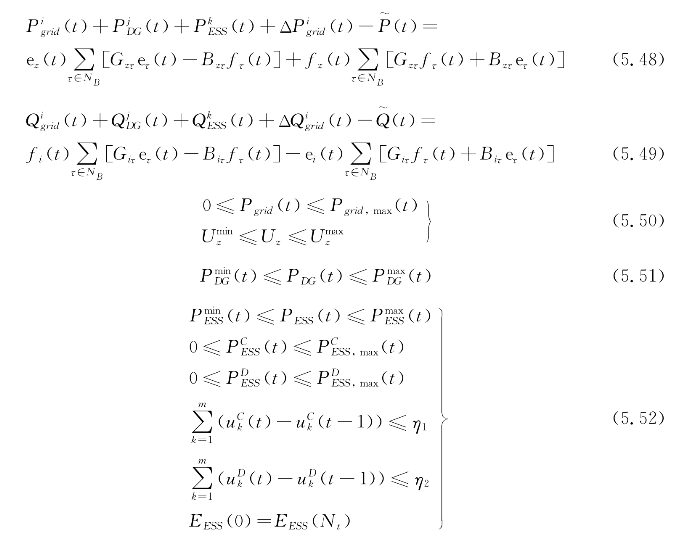
式中　NB——节点集合；

ez（t），fz（t）——节点z在t时刻电压的实部和虚部；

Gzτ，Bzτ——节点z和τ之间的互电导和电纳；

P（t）——系统在t时刻总输出有功功率；

Q——无功功率；

Pgrid，max（t）——主网在t时刻最大输出功率；

——节点z最大电压和最小电压；

——分布式电源在t时刻最小和最大输出功率；

——储能设备在t时刻最大充电、放电功率；

——t时刻储能功率的最小值和最大值；

EESS（0）——调度初始时刻的电池储能值；

Nt——实时调度时刻；

EESS（Nt）——调度结束时刻的电池储能值；

——电池k在t时刻的充电、放电状态；

η1，η2——电池在调度周期内的最大充电、放电次数。

式（5.48）、式（5.49）为系统功率平衡约束，式（5.50）为主网输出功率约束，式（5.51）为分布式电源输出功率约束，式（5.52）为储能设备约束条件。

2）实时调度优化模型

实时调度就是在日前调度的基础上，根据当前时段分布式能源系统的运行状态以及储能的充放电情况，结合超短期负荷预测，对当前各个分布式能源系统运行状态做出及时调整，使得整个配电网区域提高分布式能源有效利用率，降低系统负荷，减少运行费用，从而保证系统安全、稳定地运行。实时调度优化目标主要有两个方面：一是根据分布式能源系统运行情况，对当前系统出力情况进行修正；二是根据当前储能蓄能状态，对当前时段内储能的出力情况进行调整。

（1）分布式能源系统运行修正模型。以分布式能源运行成本最小为目标，调整或修正当前阶段已运行的分布式电源的出力（包括可控式和间歇性分布式发电），其目标函数为

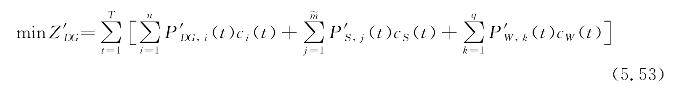
式中　——修正后的可控式分布式能源的出力；

——修正后的光伏发电出力；(www.daowen.com)

——修正后的风机机组出力；

n，m，q——各机组总个数。

（2）储能系统出力修正。根据当前阶段储能设备的运行状态来决定储能出力情况，从而对其进行修正；以储能出力波动成本最小为目标函数：

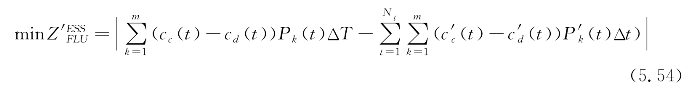
式中　——T时刻日前调度储能运行总成本；

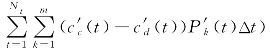——修正后实时调度储能调度运行总成本；

Pk（t），——修正前和修正后储能出力；

cc（t），——日前阶段和实时阶段充电成本；

cd（t），——日前阶段和实时阶段放电成本；

Nt——实时调度时刻。

经过修正后的分布式能源（间歇和可控）和储能需满足下列约束条件。

①修正后储能设备约束条件：

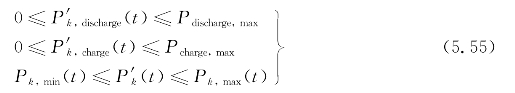
②修正后分布式电源约束条件：

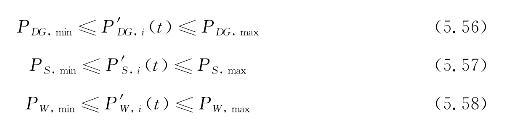
③系统总负荷平衡约束：

实时阶段的其他约束条件仍需要满足日前阶段的相关约束条件。

5.4.2.2　差分改进强国竞争算法

1）DE-ICA

ICA是Atashpaz-Gargari和Lucas于2007年提出的一种基于强国弱国竞争机制的进化算法，属于社会启发的随机优化搜索方法。ICA具有良好的全局收敛性能，能同时得到多个全局最优解。在传统的ICA中，强国竞争操作体现了强国之间的信息交互，然而，强国竞争在每一次迭代中只是将最弱的弱国归于最强的强国，该过程对每个强国的势力大小影响很小，需要多次迭代才能体现出来，强国之间缺乏更有效的信息交互，可能导致早熟。因此，本案例借鉴了微分进化思想，引入了一种微分进化算子，对ICA进行微分改进，构建DE-ICA模型。在同化操作和竞争操作之间，添加以下操作。

（1）每一个弱国以MR的概率根据式（5.60）进行微分变异：

式中　Colr1，Colr2，Colr3——随机选择的3个弱国；

F——变异因子，F∈［0，2］。

（2）对每一维度根据式（5.61）进行微分交叉：

式中　CR——交叉因子，CR∈［0，1］；

rand——随机数，rand∈［0，1］。

（3）选择采用贪婪策略，当新产生的弱国D的势力大于原来弱国的势力时，即f（D）＜f（Col），则更新弱国的位置。

2）DE-ICA模型在双阶段调度中的应用

将DE-ICA优化模型应用于分布式能源系统双阶段优化调度问题中，其求解的一般过程如下：

（1）初始化DE-ICA的参数。初始化国家数量Npop、强国数量Nimp、同化系数β、偏移方向γ和弱国影响系数ξ。

（2）控制变量编码。假设主动配电网中，分布式电源的数量为n，则分布式电源出力编码可以表示为

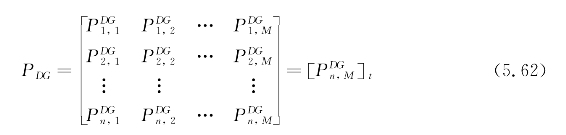
式中　——在t时刻区域j内的分布式电源i的控制功率（i＝1，2，…，n；j＝1，2，…，M）；

PESS＝——储能设备出力编码（k为储能设备数量）；

Pgrid＝——主网出力编码（Nl为馈线数量）。

因此，全部控制变量可以形成的N个国家个体为Y＝［PDG，PESS，Pgrid］N。

（3）采用DE-ICA模型进行目标函数求解，并得出最终优化结果。优化过程如图5.16所示。

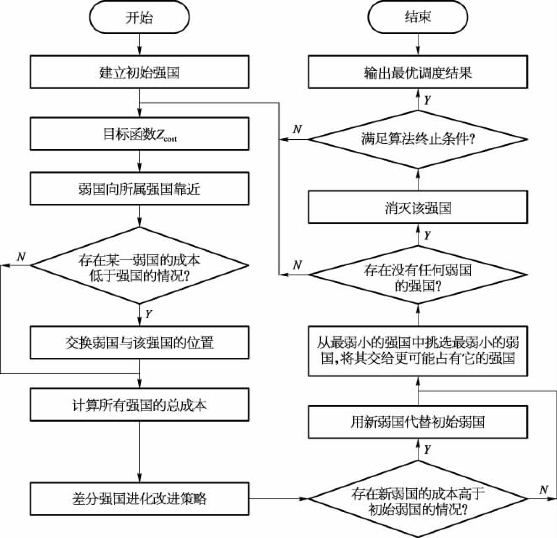
图5.16　DE-ICA模型流程图