5.2.2.1　多目标无功化

1）稳定功率特性及控制方式

如图5.5所示，us＝Us∠θs，uc＝Uc∠θc，uΔ＝UΔ∠θΔ分别为等效新能源集群的端口电压、换流站的输入电压及MMC的上、下桥臂电抗器的虚拟等电位点电压；Rsys＋jXsys为从换流站到等效新能源集群的输电通道阻抗；RT＋jXT为换流变压器的等效阻抗；RL为换流站损耗的等效电阻；XL0为换流站的桥臂电抗，当换流站为双极时c与Δ点间的电抗为XL0/4。

实际运行时，VSC-HVDC的控制对象一般为交流电压、直流电压、有功功率和无功功率。对每个VSC，进行潮流计算时需在以上4个变量中选2个，常用的组合为：①定有功功率、定无功功率控制；②定直流电压、定无功功率控制；③定有功功率、定交流电压控制；④定直流电压、定交流电压控制。对于两端VSC-HVDC来说，常见的控制方式组合为①④，②①，②③和③④。对多端VSC-HVDC来说，其控制方式组合数目更多。

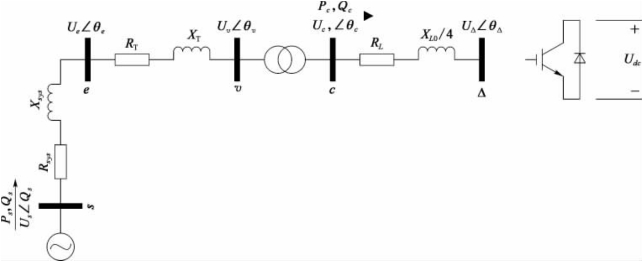
图5.5　单端MMC-HVDC示意图

当新能源集群作为孤网接入柔直电网时，需要换流站为新能源集群提供电压参考，故新能源侧换流站只能采用定交流电压、定频率控制。

图5.5中c点为平衡节点，各新能源场站均为P、Q节点。通过潮流计算可得c点有功功率Pc及无功功率Qc。故换流站损耗为

2）多目标无功优化模型

（1）目标函数。

①系统网络损耗指标。孤网接入柔直电网的新能源集群的系统网络损耗包括交流网络损耗和直流网络损耗。由于直流电压变化很小，故直流线路损耗几乎保持不变。本案例忽略直流线路损耗，引入系统网络损耗指标：

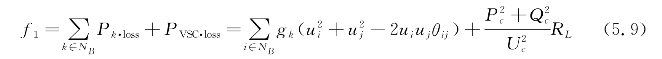
式中　ui，uj——支路i，j两端的电压幅值；

θij——相角度差；

gk——支路的电导；

Pk·loss——该支路的网损；

PVSC·loss——换流站的网损；

NB——所有支路集合。

②新能源集群无功裕度指标。为提高电压控制的响应速度，并实现新能源集群暂态电压稳定的预防控制，引入新能源集群无功裕度指标（f2取值越小，说明新能源集群无功裕度越大）：

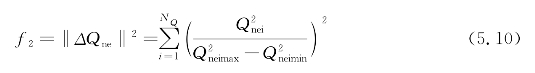
式中　NQ——新能源场站并网点的集合，i∈NQ；

Qnei——i节点的新能源场站的实时无功功率；

Qneimax，Qneimin——i节点的新能源场站的可调无功上限和可调无功下限。

③目标函数。在对以上指标归一化处理的基础上，以系统网络损耗最小和新能源集群无功裕度最大为目标，建立孤网接入柔直电网的新能源集群的无功优化模型的目标函数，即

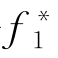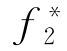式中　λ1，λ2——和在目标函数中的权重系数，满足λ1＋λ2＝1。

目标归一化处理方式如下：

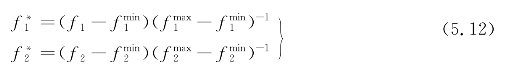
（2）约束条件。

①正常工况下交流系统约束。式（5.13）、式（5.14）为交流系统潮流方程，式（5.15）、式（5.16）为节点i上的电压和无功出力约束；式（5.17）为交流线路有功约束：

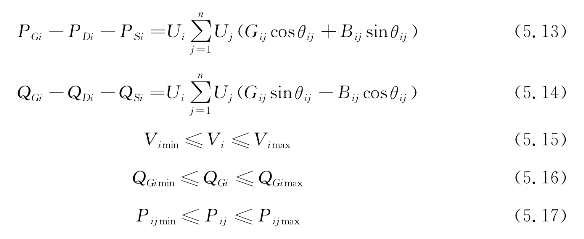
式（5.13）～式（5.17）中　PSi，QSi——交流系统由节点i向直流系统传输的有功和无功，流入直流系统为正；

PGi，QGi——节点i的发电机有功和无功出力；

PDi，QDi——节点i的有功和无功负荷；

Vimin，Vimax——节点i电压的上、下限；

QGimin，QGimax——节点i的发电机无功出力的上、下限；

Pijmin，Pijmax——交流线路ij可通过有功的上、下限。(www.daowen.com)

②正常工况下VSC-HVDC系统约束。式（5.18）～式（5.29）为换流站内部变量约束：

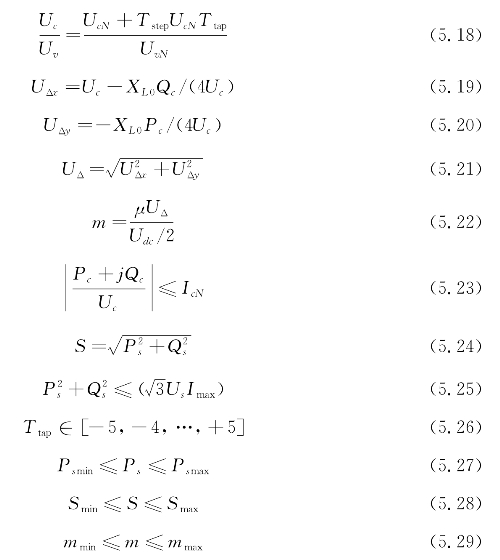
式中　Tstep——变压器抽头调节步长；

Ttap——变压器抽头位置；

Imax——可通过换流器的最大电流；

μ——直流电压利用率；

m——调制比；

Udc——单极直流电压；

S——换流变压器传输视在功率；

Psmin，Psmax——流入柔性直流系统有功的上、下限；

Smin，Smax——换流变压器传输视在功率的上、下限；

mmin，mmax——调制比的上、下限。

5.2.2.2　粒子群优化算法

1）基本粒子群算法

粒子群优化算法最初由Kennedy和Eberhart博士提出，其基本思想源于对鸟群寻觅食物行为的研究。假设在d维空间中共有m个粒子组成一个群，空间维数由待优化问题的变量数决定。将每个粒子作为d维空间里的一点，并赋予粒子一定的位置和速度，对于第i个粒子的位置和速度可分别表示为Xi＝（xi，1，xi，2，…，xi，d）和Vi＝（vi，1，vi，2，…，vi，d）。

第i个粒子迭代到目前为止的最好位置称为个体极值，记为pbest＝Pi；而全部粒子迭代到目前为止的最好位置称为群体极值，记为gbest＝Pg。各粒子速度和位置的更新公式，见式（5.30）和式（5.31）。

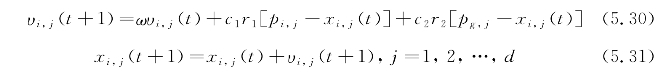
式中　i——粒子编号；

j——空间维数；

t——当前迭代次数；

w——惯性权重系数；

c1，c2——学习因子；

r1，r2——［0，1］之间服从均匀分布的随机数。

为了提高算法的收敛速度，惯性权重系数w采用线性递减的方式进行更新，如下式：

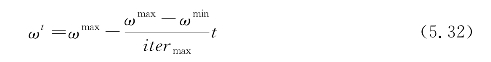
式中　itermax——最大进化代数；

wmax，wmin——wt的上、下限。

2）离散粒子群算法

Clerc提出了一种解决离散变量优化问题的离散粒子群优化（Discrete Particle Swarm Optimi-zation，DPSO）算法。DPSO算法与PSO算法的迭代寻优原理相类似，而不同的地方在于针对离散变量的优化问题其搜索空间和可行解均为离散值构成的集合。本案例仅给出速度和位置更新的基本公式，公式如下：

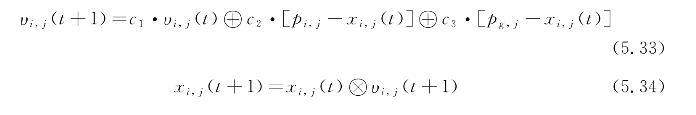
3）模型求解

对于本案例提出的孤网接入柔直电网的新能源集群多目标无功优化模型，采用粒子群优化算法进行求解，步骤如下：

（1）设置粒子群算法种群规模m、惯性权重系数w等参数，在优化模型中各变量（包括新能源场站无功出力和换流变压器抽头位置）的取值范围内随机初始化m个粒子，得到m个可行解。

（2）将每个粒子代入潮流计算，求得适应度值，并得到个体极值pbest和群体极值gbest。

（3）更新每个粒子的位置和速度：对于新能源场站无功出力变量，采用基本粒子群算法进行更新；而对于变压器抽头位置变量，采用DPSO算法进行更新。

（4）将更新后粒子代入潮流计算，检验是否满足模型的约束条件：若满足，进入步骤（5）；若不满足，在目标函数中增加相应的惩罚项。

（5）检查是否满足停止条件（达到迭代次数），若满足则停止搜索，否则转步骤（2）。