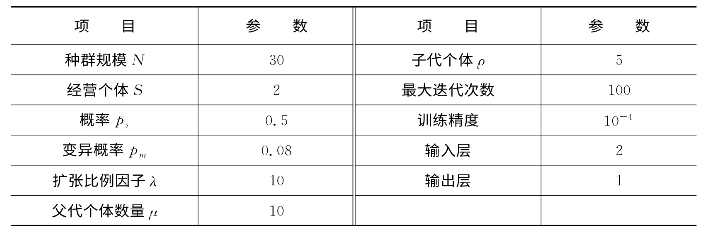
根据实验数据，可知在－20～10℃的低温段以及55～80℃的高温段，传感器误差变化呈现非线性，而在10～55℃温度区间内，传感器误差呈现线性变化。因此在10～55℃温度区间内使用直线最小二乘法进行拟合，在两端使用混合优化RBF神经网络温度补偿模型，参数设定见表5.1。

表5.1　RBF神经网络温度补偿模型参数

使用常规RBF神经网络与混合优化神经网络进行比较研究，训练误差变化曲线如图5.4所示。

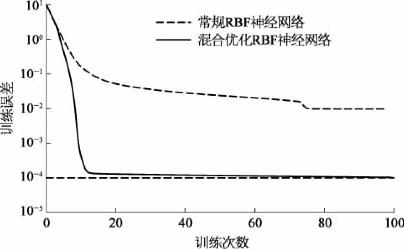
图5.4　设计曲线

经过100次训练迭代后，混合优化RBF神经网络的训练精度达到1.121×10－4，常规RBF神经网络的训练精度为1.657×10－2。可以看出，混合优化RBF神经网络比较常规RBF神经网络具有更高的训练精度和训练效率。

分别使用以下4种方法，对压力传感器在5～55 kPa压力范围以及－20～80℃温度范围内进行温度补偿：

方法1：在－20～80℃温度范围内均使用直线最小二乘法温度补偿模型。

方法2：在－20～80℃温度范围内均使用常规RBF神经网络温度补偿模型。(www.daowen.com)

方法3：在－20～80℃温度范围内均使用混合优化RBF神经网络温度补偿模型。

方法4：在10～55℃温度范围内使用直线最小二乘法温度补偿模型，在－20～10℃以及55～80℃温度范围内使用混合优化RBF神经网络温度补偿模型。

在上述4种温度补偿方法作用下，得到传感器测量误差，见表5.2。

表5.2　温度补偿方法作用下传感器测量误差

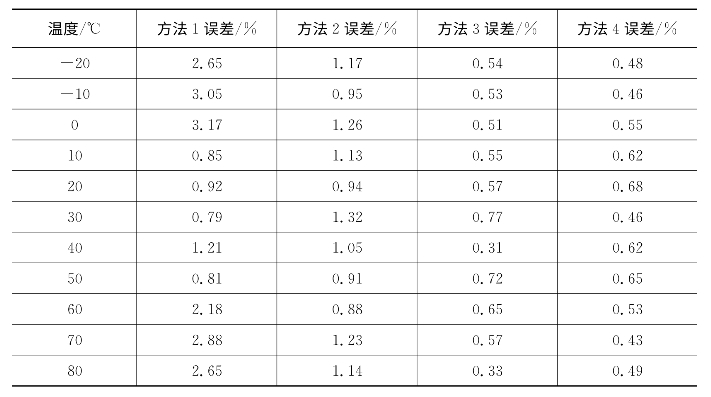
表5.2中各温度值对应的数据为使用该种温度补偿方法时，5～55 kPa各个压力点下的误差平均值。在－20～80℃温度范围内，使用温度补偿方法1的平均误差为1.92%，使用温度补偿方法2的平均误差为1.09%，使用温度补偿方法3的平均误差为0.55%，使用温度补偿方法4的平均误差为0.53%。

在－20～80℃温度范围内均使用直线最小二乘法温度补偿模型，在10～55℃温度范围内直线最小二乘法温度补偿模型显现了较好的补偿效果，误差在1%以下，但是在两端低温和高端区域，误差较大，在2%～3%之间。

在－20～80℃温度范围内均使用常规RBF神经网络温度补偿模型，显现了RBF神经网络温度补偿模型较好的拟合效果，误差控制在1%左右。

在－20～80℃温度范围内均使用混合优化RBF神经网络温度补偿模型，显现了本案例使用的混合优化算法对RBF神经网络温度补偿模型的优化性能，误差控制在1%以内。在10～55℃温度范围内使用直线最小二乘法温度补偿模型，在－20～10℃以及55～80℃温度内使用混合优化RBF神经网络温度补偿模型，误差控制在0.5%左右，与方法3相比相差不大，但是在10～55℃温度范围内温度补偿速度大大提高，提高了整体温度补偿效率。