遗传算法自提出以来，已经在科学、工程、经济等领域得到良好的应用。在20世纪90年代初遗传算法已经开始应用于给水管网优化中，在不断改进、完善的同时，其应用已经逐渐扩展到城市给水系统总体规划以及城市给水管网现状分析等课题中。本案例借鉴给水管网优化中的遗传算法的应用，将遗传算法与燃气管网水力计算相结合，提出适合于燃气管网设计的优化计算。

遗传算法模块的基本框架如图4.1所示。下面将按照程序编制的顺序来对城市燃气管网优化中的遗传算法模块进行具体介绍，管网优化设计的遗传算法实现流程如图4.2所示。

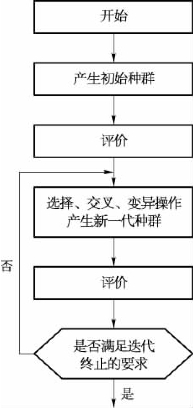
图4.1　遗传算法模块构架

1）管径编码与优化方案的表示

在遗传算法的操作中，它不对所求解问题的实际变量直接进行操作，而是对表示可行解的个体编码施加选择、交换、变异等遗传运算，通过这种遗传操作来达到优化的目的，这是遗传算法的特点之一。遗传算法通过这种对个体编码的操作，不断搜索适应度较高的个体，并在群体中逐渐增加其数量，最终寻求出问题的最优解或近似解。在遗传算法中如何描述问题的可行解，即把一个问题的可行解从其解空间转化到遗传算法所能处理的搜索空间的转化方法就称为编码。

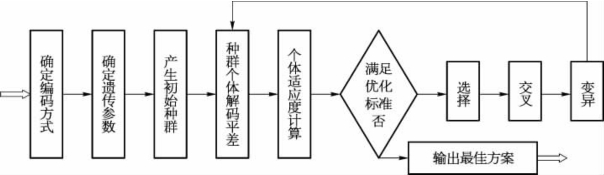
图4.2　管网优化设计中的遗传算法实现流程

具体对于燃气管网来说，编码就是将管网各管段的管径用一个数字串表达出来，而这个数字串就因此包含了管网的管径信息。

目前还没有一套既严密又完整的推导理论及评价标准帮助我们设计编码方案。借鉴前人的方法，本案例用二进制代码来表示优化问题的解。由于管网优化问题的决定变量为管径，因此必须对每一个优化过程中可能出现的标准管径分配一个二进制字符串。

例如，一个有7条管段的管网，管径分别为

76/76/133/108/89/89/108（mm）

如果用二进制编码方法，则该管网管径信息的编码为

0000｜0000｜0011｜0010｜0001｜0001｜0011

在遗传算法模块中处理的对象是二进制字符，最后得到的最优方案要解码还原成标准的工程管径。

2）产生初始群体

随机产生N个个体形成初始群体，每个个体就是由所有管段的管径按照一定顺序连接在一起的数字串，这个顺序就是管段的编号顺序。因此不同的个体代表了不同的管段管径选择情况。而个体的产生方法是：调用随机函数rand（）产生随机数，每个随机数对应着一种管径管网由多少管段组成就调用多少次随机函数。要产生N个个体，只需重复N次个体产生操作就可以了。这样就生成了我们所需要的初始群体。起初，这个初始群体中的大多数个体肯定很难满足要求，但是从这里出发，通过遗传运算，择优汰劣，最后就能选择出优秀的个体，满足目标函数的要求。

3）适应度评价标准

评价个体即计算个体的适应度。遗传算法中使用适应度这个概念来度量群体中各个个体在优化计算中有可能达到或接近于或有助于找到最优解的优良程度。适应度较高的个体遗传到下一代的概率就较大；而适应度较低的个体遗传到下一代的概率就相对小一些。遗传算法其实就是以群体中各个体的适应度为依据，通过一个反复迭代过程，不断地寻求出适应度较大的个体，最终就可得到问题的最优解或近似最优解。而度量个体适应度的函数称为适应度函数（fitness function）。适应度函数是从燃气管网优化的目标函数转换而来的：

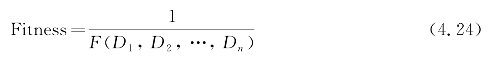
要计算个体的适应度就要知道管网经济评价函数K（Dj，Lj）的值和惩罚项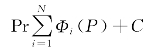的值。因为对于一个具体的个体来说，各管段管径是确定的，所以经济评价函数的大小很容易计算得到，而惩罚项的值就必须对个体进行水力计算来确定。

4）选择(www.daowen.com)

选择操作建立在对个体的适应度进行评价的基础之上。在遗传算法中，应该是更满足目标函数即适应度较高的个体将有更多机会遗传到下一代，而适应度较低的个体遗传到下一代的机会就相对较少。为实现这个机理，遗传算法使用选择算子来对群体中的个体进行优胜劣汰。事实上，选择操作就是用来确定如何从父代群体中按某种方法选取哪些个体遗传到下一代群体中的一种遗传运算。遗传算法中选择操作的方法主要有适应度比例法、期望值法、排位次序法、精华保留法等。在借鉴相关领域遗传算法的应用经验后，在前人采用的基本遗传算法的基础上采用了排序选择方法与保留精华法结合使用。排序选择方法的主要思想是对群体中的所有个体按其适应度大小进行排序，基于这个排序来分配各个个体被选中的概率。其具体操作过程是：

（1）对群体中的所有个体按其适应度大小进行降序排序，具体编程时本案例采用的排序方法是快速排序法。

（2）设计一个概率分配表，将各个概率值按上述排列次序分配给各个个体。

（3）以各个个体所分配到的概率值作为其能够被遗传到下一代的概率，基于这些概率值用比例选择（赌盘选择）的方法来产生下一代群体。保留精华法的思想是首先分别找出到目前为止遗传操作中所有出现过的个体中适应度最大的那个个体和当前群体中适应度最小的个体，然后将前者把后者替换掉。这样做的好处是能保证最优个体存活下来并指导以后的遗传操作优化的方向，而不会由于选择、变异的随机性而被淘汰。这样一代一代地重复下去，不但各代的平均适应度值逐步提高，其最优个体的适应度值也保持攀升的状态，加速了收敛过程。

5）交叉

交叉操作的设计和实现与所研究的问题密切相关，要求它既不要太多地破坏个体编码串中表示优良性的优良模式，又要能够有效地产生出一些较好的新个体模式。因此，交叉算子的设计要和编码设计统一考虑。城市燃气管网一般具有20根以上需要设计计算的主管段，如果随机概率大于或等于交叉概率就进行交叉操作，反之则不进行交叉。

6）变异

基本遗传算法中的基本位变异操作改变的只是个体编码串中的个别几个点上的值，并且变异发生的概率也比较小，所以其发挥的作用比较慢，作用效果也不明显。本案例采用的变异方法是两点互换变异，即在一个个体上随机确定要进行交换的两点，如果随机概率大于所确定的变异概率就交换这两点的值，如果没有达到变异概率的话就不进行交换。这样做可以改善遗传算法的局部搜索能力、维持群体的多样性并防止早熟现象。

7）遗传算法的运行参数

遗传算法中需要选择的运行参数主要有个体编码长度L、群体大小M、交叉概率Pc、变异概率Pm、终止代数T。这些参数对遗传算法的运行性能影响较大，但却没有理论来指导，需要从实际解决的问题出发认真选取。

（1）编码串长度L。由于是管网的优化操作所以很自然的编码串亦即个体的长度L为管网的管段总数。

（2）群体大小M。群体大小M表示群体中所含个体的数量。当M取值较小时，可提高遗传算法的运算速度，但却降低了群体的多样性，有可能会引起遗传算法的早熟现象；而当M取值较大时，又会使得遗传算法的运行效率降低。

（3）交叉概率Pc。交叉操作是遗传算法中产生新个体的主要方法，所以交叉概率一般应取大值。但若取值过大的话，它又会破坏群体中的优良模式，对进化运算反而产生不利影响；若取值过小的话，产生新个体的速度又较慢。所以，常采用自适应的思想来确定交叉概率Pc。自适应的可以随遗传操作进化的情况和个体优化的程度来确定交叉概率（随在线性能的提高增大Pc），具体如下：

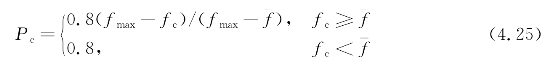
式中　fmax，——群体中最大适应度值、平均适应度值；

fc——要变异的个体适应度。

（4）变异概率Pm。若变异概率Pm取值较大的话，虽然能够产生出较多的新个体，但也有可能破坏掉很多较好的模式，使得遗传算法的性能近似于随机搜索算法的性能；若变异概率Pm取值太小的话，则变异操作产生新个体的能力和抑制早熟现象的能力就会较差。同样地，常采用自适应的思想来确定变异概率Pm，随着遗传算法在线性能的下降，可以减小变异概率Pm的取值。具体如下：

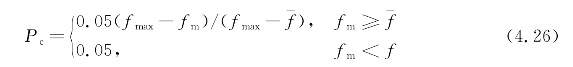
式中　fm——要变异的个体适应度。

（5）终止代数。终止代数T是表示遗传算法运行结束条件的一个参数，它表示遗传算法运行到指定的进化代数之后就停止运行，并将当前群体中的最优个体作为所求问题的最优解输出。