任何一个燃气输配系统，不仅应当在运行中安全可靠，而且要经济合理。要使燃气输配系统具有很高的经济指标，需要选择正确的管径、合理的管道定线方案以及燃气调压室、分配站的数目等。

从技术经济观点来看，任何输配系统的方案，均可用下列指标来评价投资费用即工程造价和运行费用，后者决定燃气输配成本。本案例拟采用在不考虑资金时间价值的情况下，将管网年成本设计寿命期内最小作为设计方案优化的最优准则。

燃气输配管网成本计算中，不同压力的管网其计算费用均包括管网的造价和运行费用。在计算函数形式相同，管网造价取决于管道价格和敷设费用。管网运行费用与管道埋设深度、土壤和路面性质、管道材料及其连接方式、施工机械化程度等有关。可以将管道敷设费用近似地分为与管径有关和无关两类，单位长度管道的造价C造可以表达为

因此，管网投资费用K投为

管网运行费用包括管网折旧含大修、小修和维护费用，常以占投资费用的百分数表示：

考虑到城市燃气管网的小修与维护费用主要与管道长度有关，与管径关系很小，因此，式（4.3）可进一步表达为

如果管网的投资偿还年为T′年，在不考虑资金时间价值的情况下，管网年成本Z为

由于成本计算是在网络初步确定后进行的，因而管网中各管段的长度是已知的，考虑到函数优化结果与式（4.5）中的常数项无关，则子管网年成本目标函数可以表达如下：

根据压力降方程

约束条件式可分别写为

则由式（4.6）～式（4.10）组成的优化问题中，设计（决策变量）为X＝（D1，D2，…，DM，Q1，Q2，…，QM）T。

另外根据式（4.7），得

则式（4.6）可改写为

式（4.1）～式（4.9）中　a，b，b′——管材价格系数；

f′——管网折旧费（包括大修费）占投资的百分数；

f″——管网小修和维护管理费占投资的百分数；

Lk——管长；

T′——投资偿还期，作为经济效益比较的期限。

城市燃气管网模型管内流体属于低速稳态流动，管内介质可作为不可压缩流体处理。考虑质量守恒、能量守恒、技术要求等因素，燃气管网应满足以下各种约束条件。

节点流量满足基尔霍夫第一定律，即节点流量平衡。设离开节点的流量为正，流向节点的流量为负，任一节点流入流量之和应等于流出该节点的流量之和，即任一节点的流量代数和等于零，满足质量守恒：

式中　∑gij——与节点i相关联的管段流量之代数和（t/h）；

Qi——节点的输出流量（t/h）；

N——节点个数；

j——与节点i关联的节点；

i——节点下标。

压力约束，即压力平衡。对于流体网络的每个闭合环路，满足基尔霍夫第二定律：从一个节点至另一个节点间，沿不同管线计算的压力损失相等。如规定顺时针方向介质引起的压力损失为正，相反为负，则任一闭合环路的压力损失代数之和等于零，也就是能量守恒。

式中　——属于基本环路的管段压力损失之和；

δhk——环路平差精度；

L——基本环路个数；

Bk——属于环路的管段数。

费用越小，方案越佳。燃气管网的每个用户节点，资用压力必须大于用户的允许的压力才能保证管网运行的安全性和可行性。用户节点资用压力约束表示为

式中　Pj——用户j资用压力；(www.daowen.com)

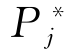——用户j设计预留压力损失；

j——用户节点下标；

u——用户数。

各用户节点的计算资用压力应大于各用户的设计预留压力，满足每个用户流量达到设计流量所需的数量。

标准管径为离散变量，并且只能在一定的范围内选取。决策变量应在工程可用的管径范围内选择。管径取值范围约束为

式中　Dmax，Dmin——标准管径序列的最大值、最小值；

Dh——h管段的可选管径。

需要指出的是在实际应用中，可以根据燃气管网的规模，适当减小可选管径的范围，例如对于较小的工程，适当缩小管径的上限公称管径，可以使可行解空间大大减小，提高算法的收敛速度并减小大量无效的计算时间消耗。

综上所述给出天然气网络成本优化的一般模型：

目标函数：

约束条件：

其中约束条件式（4.19）和式（4.20）也可以合并成如下形式：

式中　Dk——管网中管段k的直径；

Lk——管网中管段k的长度；

M——管网中的管段数；

Ki——与节点i相连的管段集合；

Kl——与环l相连的管段集合；

Khnd——由气源点到管网零点hnd的路径中管段的集合；

ZO——管网中的零点数；

ΔP——管网允许压力降（注供气点到零点的压降）；

St——某种调压站布局方案；

NP——调压站候选设置点的总数；

qi——管网中节点的负荷；

Qk——管网中管段的流量；

N——管网中的节点数；

ΔPk——管网中管段的压力降；

K——与燃气性质有关的系数；

α，β——与燃气流动状态和管道粗糙度有关的系数；

H——管网中的环数；

Ps——管网中门站（或调压站）的出口压力，即气源点压力；

Pmin，Pmax——分别为管网中允许的最小节点压力和最大节点压力。