本案例的训练样本是基于Fanger提出的PMV数学模型，在输入变量取值范围内取值，随机生成400组数据作为BP神经网络的样本数据。输入变量的取值范围如下：人体新陈代谢率M为46～232 W/m2，服装热阻Icl为0～2 clo，空气温度ta为10～30℃，空气相对湿度φ为30%～70%，空气流动速度va为0～1 m/s，平均辐射温度tr为10～40℃，人体对外做功W为0（人静坐状态）。

在数据用于训练之前，本案例对数据做了以下准备工作：数据预处理与后加工、数据划分。数据预处理即所有数据经转换后分布在比较接近的范围内，以此提高神经网络训练的效率；后加工就是将神经网络的输出数据转换成原始目标数据形式，以便于数据的后续使用；数据划分即确定样本数据被划分为训练数据、验证数据、测试数据的比例和划分方式。

本案例采用的预处理方法是对输入向量和输出向量进行归一化处理；本案例采用70%、15%、15%的比例随机划分数据，其中70%的数据用于网络训练调整权值和偏置，15%的数据用于网络验证，另外15%用于网络测试。

1）BP结构网络的确定

（1）确定输入层、输出层节点数。由PMV数学模型可知，影响PMV值的有六个因素，因此，输入层有6个神经元，分别是空气温度ta、空气相对湿度φ、空气流动速度va、平均辐射温度tr、人体新陈代谢率M、服装热阻Icl，而输出层则为1个神经元，即PMV指标值。

（2）确定隐含层层数。尽管隐含层层数的增加，可以使网络精度提高，误差也会相应降低，但是，网络结构也会随着隐含层层数的增加而变得越复杂，网络的训练时间也会增长，网络的稳定性也会有所下降，所以必须根据实际情况并权衡利弊来选择隐含层的层数。同时，研究证明，三层的BP神经网络能任意逼近任何非线性函数，因此，本案例确定使用单层的隐含层，即利用BP神经网络建立PMV指标的3层神经网络预测模型。

（3）确定隐含层节点数。隐含层节点数目的确定方法虽有很多，如经验公式法、单元合并与删除法等，但其适用性均不强，因此，本案例采用尝试法，经具体环境反复尝试后，最终确定隐含层节点数为10个，所以BP神经网络的结构最终确定为6-10-1结构。(www.daowen.com)

（4）其他参数确定。除上述网络结构的主要参数外，还确定了BP神经网络的最大步数为1 000，学习率为0.01，学习目标为0.001。

2）模型仿真

本案例在MATLAB 7.11版本下，采用MATLAB语言编写算法程序，结合MATLAB神经网络工具箱，利用上述的参数设置及样本数据构建了基于BP神经网络的热舒适度预测模型。仿真结果如图3.18所示。图3.18给出了PMV指标的实际输出与期望输出比较曲线，并给出了两者的绝对误差图。图3.18的横坐标代表输入样本数组，即每一数组代表一个热舒适工况，由影响PMV值的六个因素的相应数值组成，纵坐标代表相应工况的PMV值。

从图3.18的仿真结果可知，利用简单的BP神经网络建立的热舒适度预测模型，其收敛速度较慢，且预测误差也较大。产生这些问题的原因，是传统的BP神经网络是一种局部搜索的优化方法，且其训练算法实质为梯度下降算法。因此，算法的收敛速度慢，且易陷入局部最小；同时，该算法对网络初始值、学习效率等较敏感，训练结果不稳定。因此，基于BP神经网络的PMV预测模型，虽然解决了PMV数学模型的非线性计算问题，但因BP神经网络算法对网络初始权值和偏置较敏感且易陷入局部最小，该预测模型算法收敛速度慢且预测精度不高。这也是之后需要进行改进的方向。

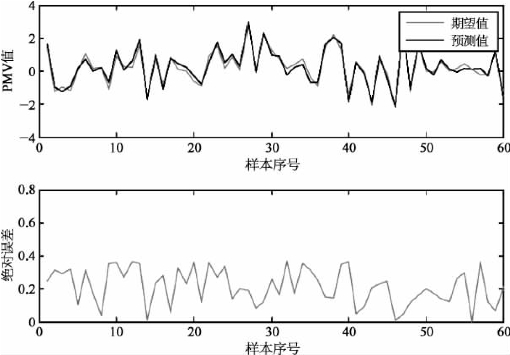
图3.18　预测结果图