3.5.2.1　热舒适度预测建模方法介绍

热舒适度与环境变量和人体参数等多种因素有着复杂的非线性关系，无法直接测量，更无法直接用于空调的实时控制系统中。因此，建立一个能正确评价、准确预测室内环境热舒适度，并能用于空调实时控制系统中的热舒适度预测模型，成了学者们需要解决的一个重要问题，同时也是本案例的主要任务之一。

自20世纪80年代以来，传统的PMV模型一直是一个国际标准，被广泛用于舒适度预测与控制研究中，因此，本案例模型也是在这一传统模型的基础上建立的。然而，PMV指标的求值过程是一个复杂的非线性过程，需经过繁琐的迭代运算，不便于空调系统的实时控制应用。因此，需要建立一个能应用于实时控制系统的PMV预测模型，来替代这一计算复杂且不能应用于实时控制系统的传统数学模型。

随着智能优化算法的发展，BP神经网络因其算法简单，具有很强的非线性逼近能力，被广泛应用于模式识别、函数逼近、预测等工程实际中。基于BP神经网络的舒适度预测算法，降低了网络训练的复杂度和预测误差，解决了PMV数学模型的非线性计算问题，但因BP神经网络算法对网络初始权值和偏置较敏感且易陷入局部最小，该预测模型算法收敛速度、预测精度有待进一步提高。针对存在的这些问题，本案例在BP神经网络算法的基础上做出了相应改进。

3.5.2.2　BP神经网络模型

如本书第2.3.3.2节所述，BP神经网络是一种以误差逆传播算法作为训练算法的多层前馈网络，也是目前发展最成熟、应用最广泛的神经网络之一。BP神经网络作为多层感知器神经网络的典型代表，具有结构简单、便于理解等特点，因此，目前绝大部分的神经网络均采用的是BP神经网络或者是其结构形式的变种，应用非常广泛。

图3.15所示即为BP神经网络结构示意图，是典型的多层网络结构，分别由输入层、隐含层、输出层组成，其中输入层与输出层均为单层结构，隐含层有单层与多层之分。BP神经网络是以最速下降法作为学习规则，通过对误差的反向传播来调整网络的权值和阈值，最终使网络的误差平方和降至最小。

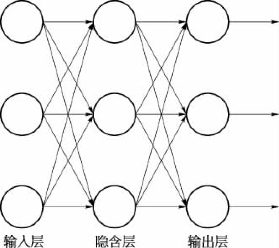
图3.15　BP神经网络结构

3.5.2.3　热舒适度评价指标介绍

热舒适度评价指标是以人体生理学、建筑学、物理学为基础，表征了人体热舒适度与影响室内热环境的多种因素之间的关系，具有明确的计算方式。目前，常用的热舒适度评价指标有如下几种：有效温度（ET），新有效温度（ET*），新标准有效温度（SET*），预测平均投票数（Predicted Mean Vote，PMV）等。这些指标有各自的优点，也有缺陷，因此，评价指标在使用时，具有一定的使用范围，同时也存在着一定的局限性。

本案例以PMV作为评价指标。PMV是丹麦的范格尔（P.O.Fanger）教授提出的表征人体冷热感（热反应）的评价指标，代表了大多数人在同一室内环境下的冷热感觉的平均。PMV热舒适度指标模型是在热平衡与体温调节的理论基础上得出的。人体是通过调节皮肤血流量、出汗、打冷颤等生理过程来保持身体产热量与失热量之间的平衡。达到热中性感觉的首要条件是保持热平衡，Fanger认为，通过人体的体温调节，即便是处于不舒适的热环境中，人体也可以在环境参数的较大变化范围内获得热平衡。

PMV模型作为目前最具代表性且应用最广泛的热舒适度评价指标模型，有明确的计算关系表达式。该指标是关于四个环境变量和两个人体相关变量的函数，变量分别是空气温度、空气相对湿度、空气流动速度、平均辐射温度、人体活动程度、衣服热阻。图3.16为各个变量与PMV值的示意图，PMV指标的取值范围是－3到3，分别对应着人从冷到热的感觉，其中0代表冷热感适中状态。

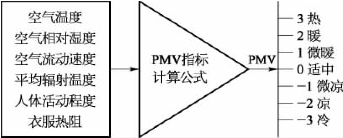
图3.16　PMV与热感觉示意图

PMV的数学模型为：

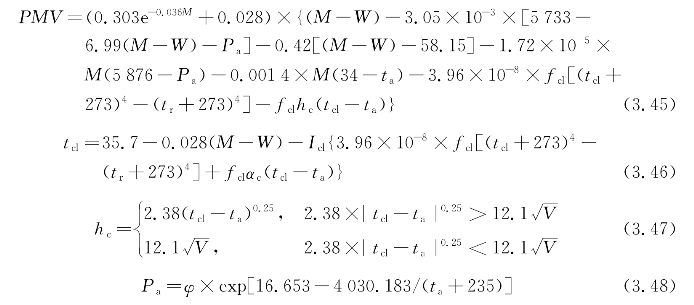
上几式中　M——人体新陈代谢率；

W——人体对外做功；

ta——空气温度；

Pa——人体周围水蒸气压力；

fcl——服装表面积系数；

tcl——服装表面温度；

tr——平均辐射温度；

hc——对流传热系数；

Icl——服装热阻；

va——空气流动速度；(www.daowen.com)

φ——空气相对湿度。

当人体对外做功为0时，PMV可表示为如下：

3.5.2.4　BP神经网络的学习算法

假设BP神经网络结构为简单的三层结构，如图3.14所示，输入层有I个节点，即对应着BP网络的I个输入；输出层有K个节点，对应着网络的K个输出；隐含层节点数的确定需根据具体情况而定。其中，输出层输出Ok和隐层输出Hj表示如下：

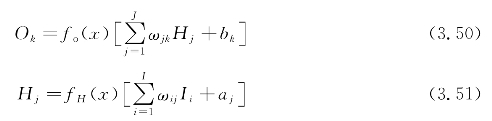
式中　ωjk——隐层节点j与输出层节点k的连接权值；

ωij——输入层节点i与隐层节点j的连接权值；

bk——输出层节点k的阈值；

aj——隐层节点j的阈值；

fo（x）——输出层的激活函数；

fH（x）——隐层的激活函数。

误差反向传播：当输出层的实际输出值与期望值不符时，误差从输出层向隐含层、输入层逐层反传，并按误差梯度下降的方式逐层修正各连接权值和阈值，直至样本均方误差降至最小为止的过程。误差函数表示如下：

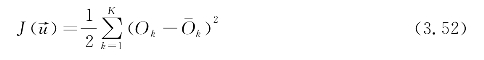
式中　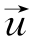——网络所有权值和阈值的向量；

Ok——第k个输出节点的期望输出值。

其中，误差反向传播过程中的权值和阈值按下式调整：

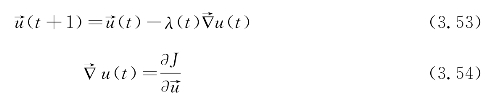
式中　λ——学习效率。

样本均方误差计算公式为

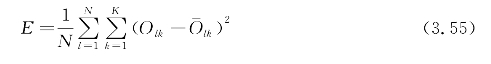
式中　n——样本总数；

Olk，——第l个样本第k个输出节点的实际输出值和期望值。

BP神经网络算法在应用时的基本逻辑思路由图3.17中的算法流程图表示。

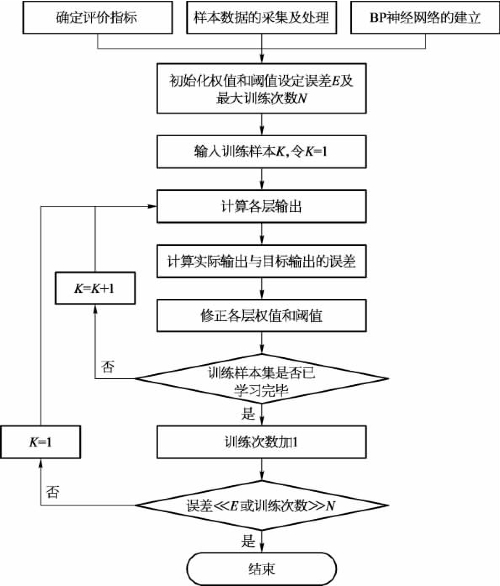
图3.17　BP算法流程图