2.3.3.1　多项式补偿

由图2.19和图2.20也可以看出，陀螺温度与陀螺原始输出具有一定的线性关系，但并非完全线性，因此可以首先选择利用最小二乘法建立多项式二次模型来进行补偿。

温度模型如下：

利用上述模型，对温度实验中得出的数据｛U（ti），ti｜i＝1，2，…，n｝应用最小二乘法建立误差多项式。确定模型中的系数ai（i＝1，2，…，n）。并且ai（i＝1，2，…，n）使得均方和误差∑ni＝［U（ti）－B（ti）］2取得极小值。经过解算后，得到如下补偿多项式：

式中　B（T）——陀螺输出补偿量；

T——温度。

补偿后输出Uc（Ti）＝U（Ti）－B（Ti），曲线如图2.21所示。由上述论述可以看出，多项式补偿方法较为简单，而且取得了一定的效果。

图2.21　补偿前后陀螺输出曲线

2.3.3.2　BP神经网络补偿

BP（back propagation）网络由Rumelhart和McCelland于1986年提出，是一种多层前馈网络，按误差逆传播算法进行训练。BP网络在无须事前揭示描述这种映射关系的数学方程的情况下，能够学习和存储大量的输入-输出模式映射关系。它的学习规则是通过网络的反向传播来不断调整网络的权值和阈值，使输出误差最小。BP神经网络结构包括输入层（input）、隐层（hidelayer）和输出层（output layer）。每层节点的输出只影响下一层节点。各层节点的传递函数通常为双曲（tansigmoid、logsigmoid）函数，输出层节点的传递函数一般为纯线性函数（pureline）。BP网络模型的结构如图2.22所示。

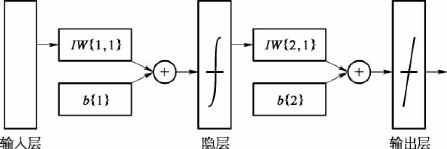
图2.22　BP网络模型结构

在图2.22中，IW｛1，1｝、b｛1｝表示隐层3个神经元的权值、阈值；IW｛2，1｝、b｛2｝表示输出层神经元的权值、阈值。

在建立BP神经网络时，本案例中使用了3层神经网络模型，这是因为根据Kolmogorov定理，3层前向神经网络能够模拟任意连续函数，而且能够以任意的精度完成。

同时鉴于训练样本较大，将样本都进行了归一化处理，使样本值范围变为［－1，1］，而且在隐层只选用了3个神经元，以提高训练的速度。

在隐层的传递函数选择上，使用正切双曲函数（tansig），而输出层则选用纯线性函数（pureline）。

在室温条件下，陀螺从冷却开始上电工作，通过编写上位机程序来测量输出数据。将连续工作4 000 s得到的陀螺温度、轴向输出数据作为一个样本，在进行了多次重复实验后，选取其中2个样本的温度、陀螺输出，1个作为训练样本，另外1个样本作为验证样本。

利用训练样本对BP网络进行训练，各个训练参数设定如下：

net.trainParam.epochs＝2 000；//最大训练步数为2 000步(www.daowen.com)

net.trainParam.show＝50；//每训练50次，显示一次训练结果

net.trainParam.lr＝0.05；//学习系数为0.05

net.trainParam.mc＝0.9；//动量因子为0.9

net.trainParam.goal＝0.01；//期望的误差平方和为0.01

根据上述设置进行仿真并补偿，得到的结果如图2.23所示。

从仿真曲线和结果可以看出，该BP网络模型对于自身样本的补偿效果显著，说明该模型对微机械陀螺进行补偿切实可行。

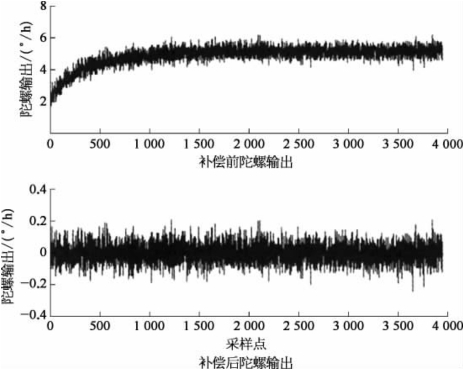
图2.23　补偿前后陀螺输出

2.3.3.3　算法比较

将BP神经网络与最小二乘法补偿后误差方差进行对比，见表2.9。

表2.9　神经网络最小二乘法多项式补偿后误差方差对比

根据以上统计结果，采用传统的最小二乘法二阶补偿所得到的误差方差为1.2×10－5，而采用BP神经网络补偿得到的误差方差为2.5×10－6，比最小二乘法补偿的误差方差要小很多，因此，其拟合以及补偿的效果都要好于最小二乘多项式拟合。

总结以上两种方法，各自的优缺点如下：

（1）由表2.9可以看出，在一般情况下，多项式补偿误差比神经网络的补偿误差可以大一个数量级。因此在精度上略逊一筹。

（2）神经网络算法具有很大的随机性，相同的数据、训练参数以及训练次数却可能得到不同的结果，而多项式方法则具备一定的规律性。

（3）神经网络能够处理那些含有较大非线性甚至随机关系的数据系列，而多项式能较为准确拟合的是曲线的主要趋势。

（4）由于算法本身的不完善，当温度范围超过测量数据的范围时，用神经网络进行补偿有可能出现较大的误差。

（5）神经网络则并不依赖精确数学模型，而多项式拟合使用的是精确数学模型，这也使得神经网络算法能够逼近、拟合任意函数，因此也具有更广泛的应用范围。

综上所述，最小二乘法是一种简单且容易实现的方法，一般来说精度可能比神经网络要低，而神经网络算法和结构都较为复杂，训练参数的调整还要依赖经验，因此在应用中存在不少问题。