2.2.2.1　机器人的动力学描述

依据拉格朗日（Lagrangian）公式，对机器人建立的动力学方程表述如下：

式中　q∈Rn——机械臂的位形变集合；

u（t）∈Rn——机械臂的关节输入的扭矩向量；

D（q）∈Rn×n——机械臂的惯性矩阵；

h（q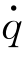，）∈Rn——机械臂的哥氏力向量和离心力；

g（q）∈Rn——机械臂的重力作用向量。

定义状态向量，系统的状态方程表述如下：

式中　；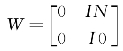

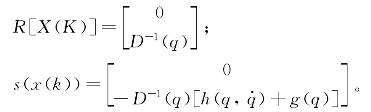
选取终端变量作为输出，输出方程表达式为

2.2.2.2　自适应控制神经网络学习算法及实现

对NNI首先进行离线辨识，运行一定程度后，再采用在线学习的方式，以达到加快学习过程的目的，具体如图2.16所示。

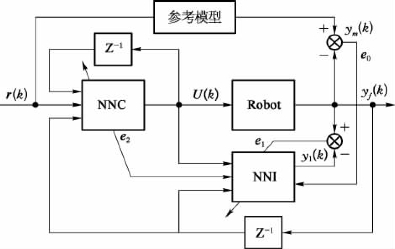
图2.16　机械臂的自适应控制神经网络参考模型方框图

在该过程中，NNI把e1的值反传回各自身的神经元，进行权值的修正；NNI在误差e0通过后，可以经过运算计算出e2，再进行NNC的权值修正。

参考模型是一个稳定的线性定常系统：

(www.daowen.com)

式中　；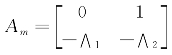

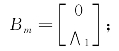
∧1和∧2——含有ωi项和2ξiωi项的n×n对角矩阵。

误差表示用Ei（i＝0，1），NNI和NNC的算法如下。

NNC的整定指标：

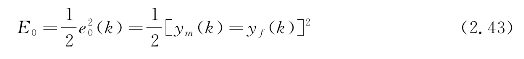
NNC的学习算法可以得到

NNI的整定指标：

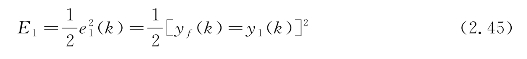
和NNC的求取方法一样，可得

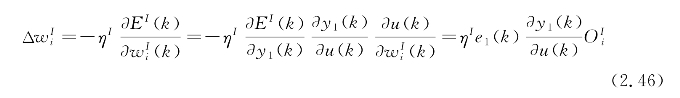
为了完成上述计算过程，可以分为以下步骤：

（1）自动从片外的权值存储器读出初始权值、阈值至片内权值的各个RAM。

（2）前向网络开始计算，并输出个节点的结果。

（3）反传和更新模块接收各节点的计算结果，计算出误差和修正后的权值、阈值。

（4）判断误差大小和训练次数。

（5）修正后的权值、阈值写入各个RAM。

（6）重复第（1）至（5）步，直至误差足够小或达到指定训练次数。

（7）将训练好的复合系统需求的权值、阈值存入片外权值存储器备用。