2.1.3.1　模型假设和符号说明

模型的符号说明见表2.2。其余符号在文中给出。

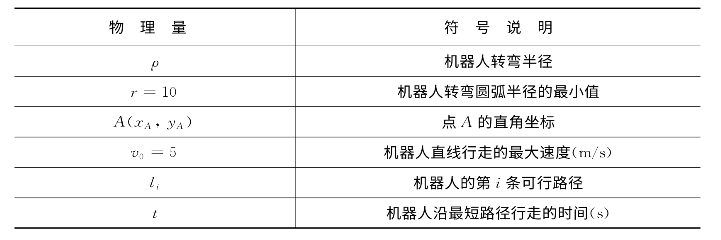
表2.2　符号说明

为了简化问题，做如下假设：

（1）把机器人抽象成一个质点。

（2）所有障碍物为静态的，其位置固定不变。

（3）机器人绕过障碍物顶点时转弯圆弧半径为10个单位。

（4）机器人直线行走速度与圆弧行走速度之间的转换都是瞬间完成的。

（5）机器人的直线行走速度和圆弧行走速度都是匀速。

（6）在直线阶段机器人以最大速度行走。

（7）机器人不能直线转弯。

（8）机器人绕过中间目标点时转弯圆弧半径至少为10个单位。

（9）在最速路径模型中，机器人转弯圆弧半径至少为10个单位。

（10）长度单位为“单位”，时间单位为“s”。

2.1.3.2　建模准备

设长方形的长大于宽，将长方形障碍物9的长与宽的值交换，即长为120，宽为60。

设曲线弧的极坐标公式方程为ρ＝ρ（θ），θ1≤θ≤θ2，则曲线弧长为

1）最短路径定理

定理2.1　如图2.3所示，已知点O、点A为障碍物（三角形、矩形、平行四边形）外一点，从点O出发，绕过障碍物顶点S到达点A，以点S为圆心、r为半径画圆，分别过O、A作圆S的切线，切点分别为D、E点，则路径ODEA是从点O出发的、从上面绕过障碍物到达点A的最短路径。

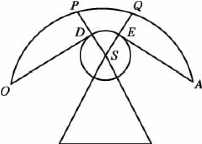
图2.3　绕过障碍物顶点的最短路径

证明：设曲线L为从圆S的上面绕过的路径，连接SD并延长交曲线L于P点，连接SE并延长交曲线L于Q点，显然有

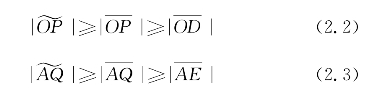
其中，等号当且仅当P点与D点重合、Q点与E点重合、OP与AQ为直线时成立。

再以S为极点建立极坐标系，曲线L的极坐标方程为ρ＝ρ（θ），θ1≤θ≤θ2，θ1、θ2分别为Q点和P点的极角（也是E点和D点的极角）。由式（2.1）得

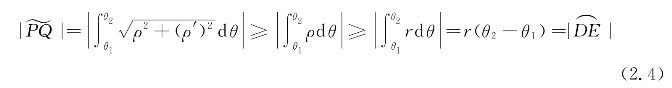
式（2.4）中的等号当且仅当ρ≡r，即路径PQ与圆弧DE重合时成立。

由式（2.2）～式（2.4）可知，路径ODEA是从上面绕过障碍物的最短路径，证毕。

2）向量伸缩和旋转变换

已知向量，把向量的长度变换为原来的k（k≠0）倍后的向量为，则

已知向量，把向量顺时针旋转θ角度，旋转后的向量为＝（xB，yB），则

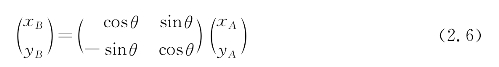
如果是逆时针选择θ角度，则

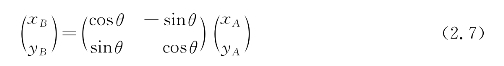
3）切点坐标及切线长度

（1）点到圆的切线。如图2.4所示，从圆O外一点向圆做切线，切点分别为B、C，设O（x0，y0），A（xA，yA），B（xB，yB），C（xC，yC），向量看作由向量顺时针旋转和伸缩变换而来，向量看作由向量逆时针旋转和伸缩变换而来，于是根据式（2.5）～式（2.7），得

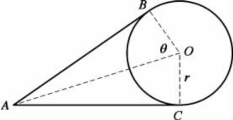
图2.4　圆外一点与圆相切

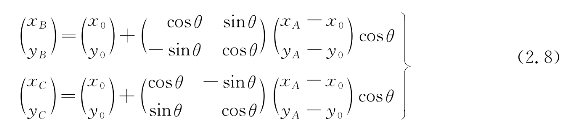
其中　

显然，。

切线长度为

（2）两圆外公切线。如图2.5所示，设两圆的圆心分别为O1（x1，y1），O2（x2，y2），半径分别为r1，r2，不妨设r1≥r2，当｜O1O2｜＞r1－r2时，有两条外公切线AB和CD。设A（xA，yA），B（xB，yB），C（xC，yC），D（xD，yD）。

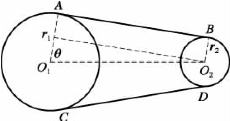
图2.5　两圆外公切线

向量看作由向量逆时针旋转和伸缩变换而来，向量看作由向量顺时针旋转和伸缩变换而来，则

其中　

显然。

切线长度为

当｜O1O2｜＝r1－r2时，只有一条外公切线。当｜O1O2｜＜r1－r2时，没有外公切线。

（3）两圆内公切线。类似地，当｜O1O2｜＞r1＋r2时，有两条内公切线AB和CD，如图2.6所示。向量看作由向量逆时针旋转和伸缩变换而来，向量看作由向量顺时针旋转和伸缩变换而来，于是公切点的坐标分别为

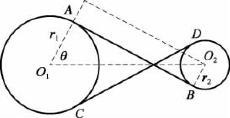
图2.6　两圆内公切线

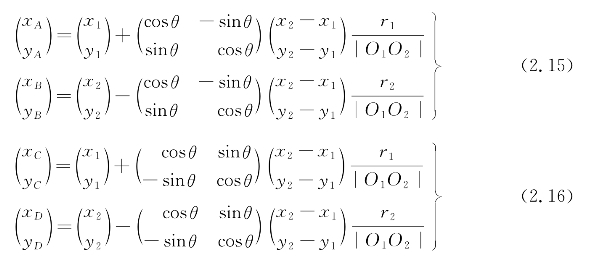
其中　

显然，。

切线长度为

当｜O1O2｜＝r1＋r2时，只有一条内公切线。当｜O1O2｜＜r1＋r2时，没有内公切线。

4）禁区的数学表示

将障碍物及其周边安全距离10单位所构成的区域称为该障碍物的禁区。

将所有障碍物禁区的并集称为机器人行走禁区，记为Ω。

（1）三角形障碍物禁区的解析表达式。如图2.7所示，设三角形顶点坐标分别为A（xA，yA），B（xB，yB），C（xC，yC），根据式（2.11）和式（2.12）可以求得切点D、E、H、K、F、G的坐标，分别记为D（xD，yD），E（xE，yE），H（xH，yH），K（xK，yK），F（xF，yF），G（xG，yG），则切线DE、FG、HK的直线方程为

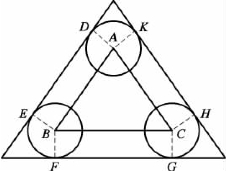
图2.7　三角形障碍物

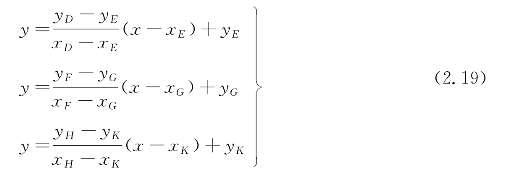
于是三角形障碍物禁区可表示为

其中

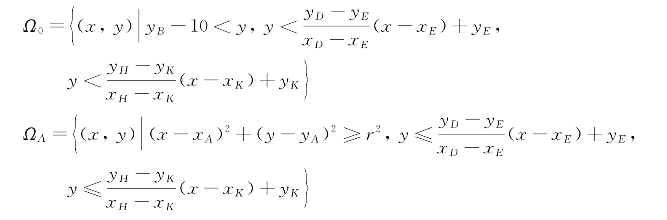
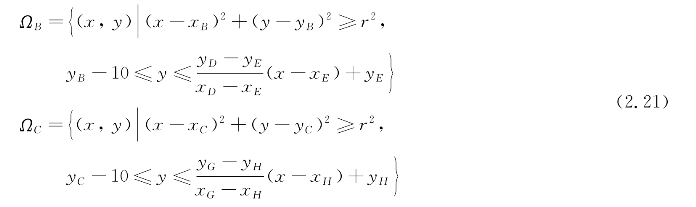
（2）长方形（或正方形）障碍物禁区的解析表达式。如图2.8所示，设长方形左下顶点坐标为A（xA，yA），长为a，宽为b，长方形障碍物禁区可表示为

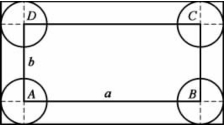
图2.8　长方形障碍物

其中

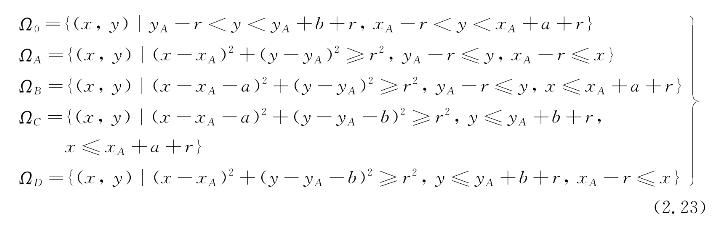
如果是正方形障碍物，则取边长a＝b即可。

（3）平行四边形障碍物禁区的解析表达式。如图2.9所示，设平行四边形ABCD的左下和左上顶点坐标分别为A（xA，yA），B（xB，yB），其余两个顶点的坐标分别为C（xC，yC），D（xD，yD），根据式（2.11）和式（2.12）可以求得切点E、F、G、H的坐标，分别记作E（xE，yE），F（xF，yF），G（xG，yG），H（xH，yH），则切线EF、GH的直线方程分别为

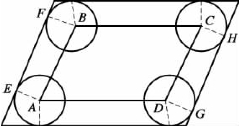
图2.9　平行四边形障碍物

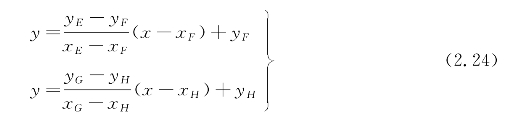
于是平行四边形障碍物禁区可表示为

其中(www.daowen.com)

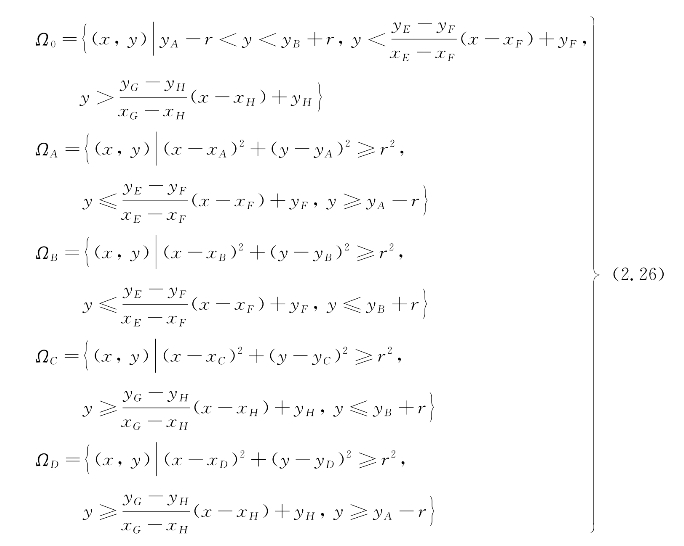
（4）圆形障碍物禁区的解析表达式。设圆心坐标为O（x0，y0），半径为R，圆形障碍物禁区可表示为

（5）机器人可行区域。设平面区域的静态障碍物一共有n个，各个障碍物禁区为Ωi，i＝1，2，…，n，则机器人行走禁区为。

设机器人活动场景范围为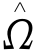，则，0≤y≤800｝；

设机器人的可行区域为Ω，则。

（6）机器人可行路径。设机器人某一段行走路径（直线段或圆弧）构成的点集为A，若A⊃Ω，则称该路径为可行路径。

2.1.3.3　最短路径模型

根据机器人行走目标点个数不同，分为单目标点和多目标点分别来讨论。

1）单目标点的最短路径模型

建模思路：从出发点到目标点存在多条可行路径，每一条可行路径由若干直线段和若干圆弧组成，经过统计汇总各条路径的长度，再比较就可以找到最短长度的可行路径。

（1）模型建立。根据假设（1）～（3），可以设计若干条可能的最短可行路径。设机器人从出发点到目标点有m条可行路径l1，l2，…，lm，第i条可行路径li由ki条直线段长度ai和hi条圆弧长度bi组成，则第i条可行路径li的总长度为

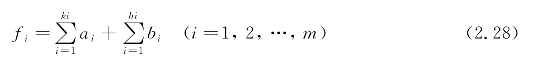
将fi从小到大排序，选出最小的fi，所对应的路径li，就是最短路径。

根据假设（4）～（6），相应的行走时间为

式中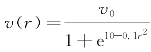，，r为转弯半径。

（2）模型求解。从O→A有多条可行路径：经过计算和筛选，最短路径如图2.10所示，最短距离为471.037 2，行走时间为96.017 6 s，其余结果见表2.3。

从O→B有多条可行路径：经过计算和筛选，最短路径如图2.10所示，最短距离为853.700 1，行走时间为156.809 0 s，其余结果见表2.4。

从O→C有多条可行路径：经过计算和筛选，最短路径如图2.10所示，最短距离为1 088.195 2，行走时间为213.295 8 s，其余结果见表2.5。

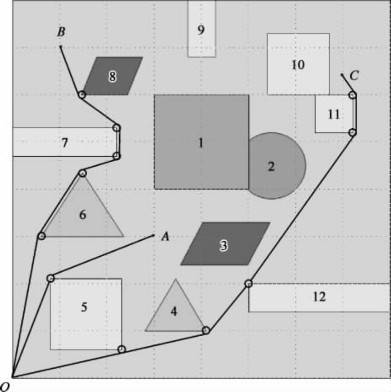
图2.10　单目标点最短路径

表2.3　OA的最短路径

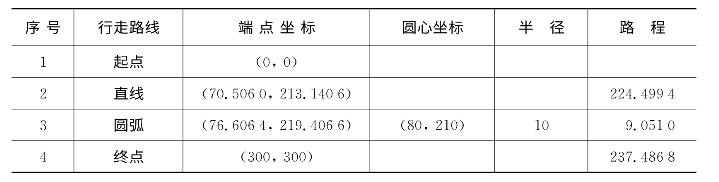
表2.4　OB的最短路径

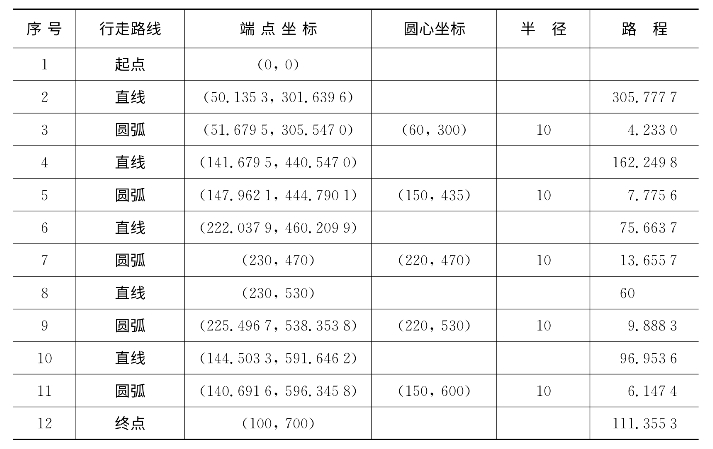
表2.5　OC的最短路径

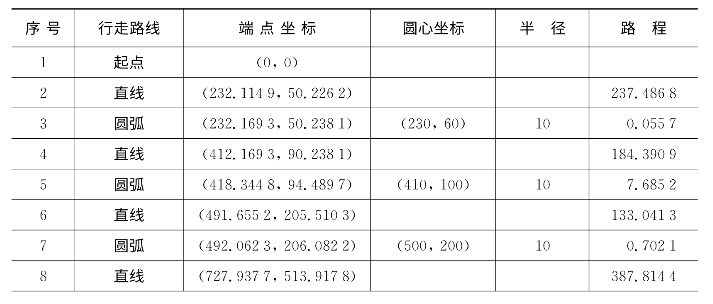
续　表

2）多目标点的最短路径模型

建模思路：在多目标点的最短路径模型中，机器人需要依次经过若干中间目标点。根据假设（7），机器人不能折线转弯，故需要确定机器人在绕过中间目标点的转弯圆弧的圆心和半径。根据中间目标点转弯圆弧与相邻两障碍物顶点圆弧的公切线类型的不同，需要分3种情况讨论。

已知点A（xA，yA）为中间目标点，机器人从某障碍物顶点B（xB，yB）出发绕过A点到达另一个障碍物顶点C（xC，yC），需要确定绕过A点的圆弧圆心和半径。设该圆心为D（xD，yD），半径为rD，根据假设（8），rD≥r。机器人绕过A点的公切线分别为EF和GH，它们的坐标分别为E（xE，yE），F（xF，yF），G（xG，yG），H（xH，yH），根据公切线的类型不同，分以下3种情况讨论。

（1）同时外切。在图2.11中，EF、GH都是外公切线。

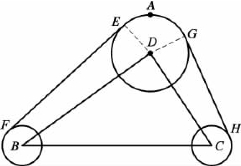
图2.11　同时外切

根据式（2.13）和式（2.14）可得切线长度｜EF｜、｜GH｜和θE，θG，设∠BDC＝α，则根据向量夹角余弦公式，得

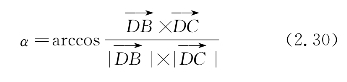
圆弧长度为

根据机器人路径最短的目标，得目标函数为

下面分析约束条件。根据点A在圆D上，得

半径约束为rD≥r，｜BD｜＞rD－r，｜CD｜＞rD－r，汇总，得。

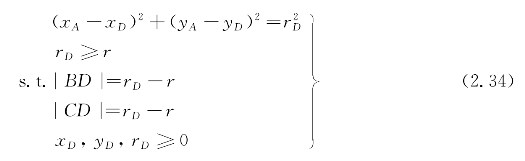
（2）同时内切。在图2.12中，EF、GH都是内公切线。

根据式（2.17）和式（2.18）可得切线长度｜EF｜、｜GH｜和θE，θG，优化模型为。

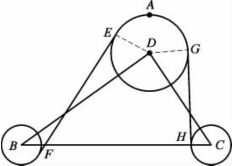
图2.12　同时内切

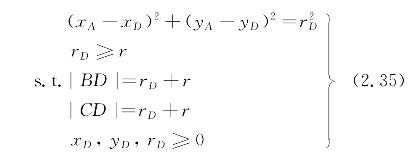
（3）外切和内切同时存在。在图2.13a中，EF是外公切线，GH是内公切线。

根据式（2.13）和式（2.14）可得切线长度｜EF｜和θE，根据式（2.17）和式（2.18）可得切线长度｜GH｜和θG，优化模型为，使得

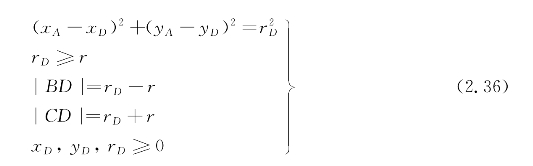
在图2.13b中，EF是内公切线，GH是外公切线。

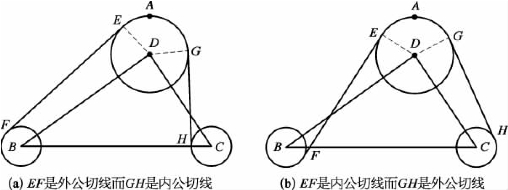
图2.13　外切和内切同时存在

根据式（2.17）和式（2.18）可得切线长度｜EF｜和θE，根据式（2.12）和式（2.13）可得切线长度｜GH｜和θG，优化模型为。使得

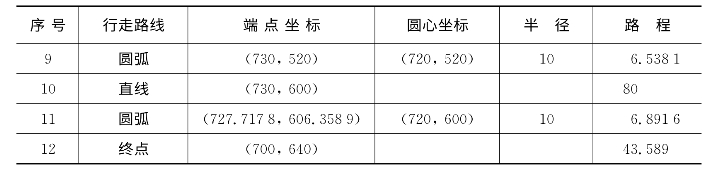
（4）模型求解。从O→A→B→C→O有多条可行路径，经过计算和筛选，最短路径如图2.14所示，最短距离为2 732.727 5，行走时间为522.245 0 s，其余结果见表2.6。

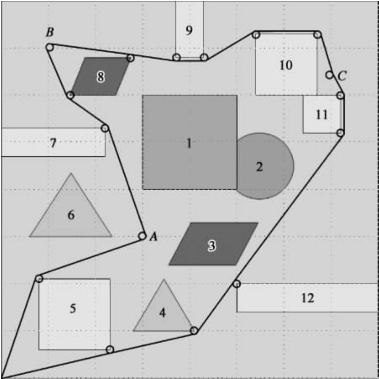
图2.14　多目标点的最短路径

表2.6　OABCO的最短路径

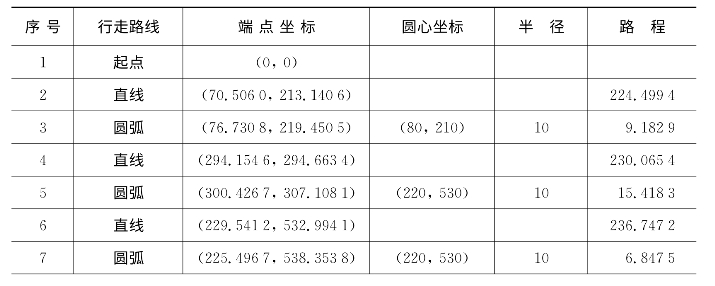
续　表

2.1.3.4　最速路径模型

由于转弯半径越大，行走速度越大，行走时间越小，但行走路径也越大，所以路径最短与时间最短是互相矛盾的，机器人沿着最短路径行走所用的时间不一定是最少的。

建模思路：将直线段路径总和除以直线段速率得到直线段时间总和，将转弯路径总和除以转弯速率得到转弯时间总和，这两个时间总和再相加，得到总时间，作为目标函数求最小值即可确定行走路径，这里只讨论单目标点的最速路径模型。

1）模型建立

如图2.15所示，设点O（xO，yO），A（xA，yA），点C（xC，yC）为障碍物5的左上顶点，机器人转弯圆弧的圆心为B（xB，yB），半径为ρ，机器人沿着转弯圆弧从障碍物5左上顶点绕过，到达目标点A。设切线分别为OD和AE，切点坐标分别为D（xD，yD），E（xE，yE），切线长度分别为｜OD｜，｜AE｜，转弯圆弧长度为｜DE｜。

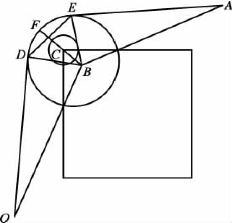
图2.15　最速路径模型

根据式（2.9），得

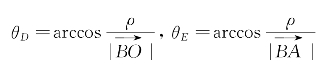
根据式（2.8），得

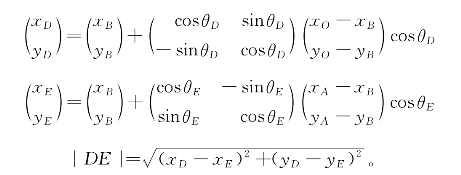
根据式（2.10），得

转弯圆弧长度为

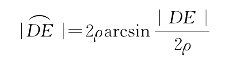
目标函数为最短行走时间，即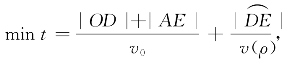其中，v（ρ）＝。

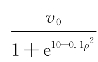下面分析约束条件。

根据2.1.3.1节下假设（9），机器人转弯半径至少为r，得

点D、E在圆B上，即

汇总，得

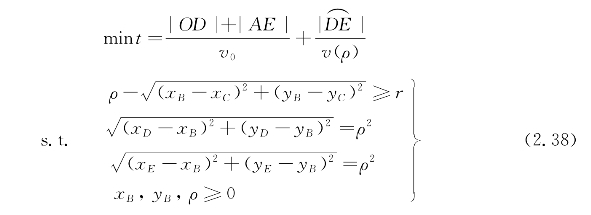
2）模型求解

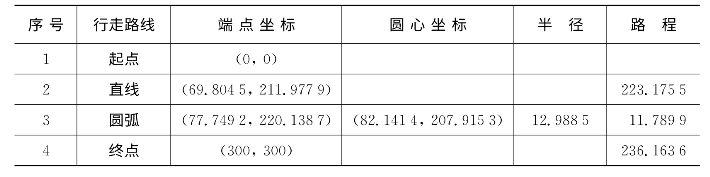
将已知条件代入式（2.35），使用LINGO软件求解，得最短时间为94.23 s，总路程为471.129 0，其余结果见表2.7。

表2.7　O→A的最速路径