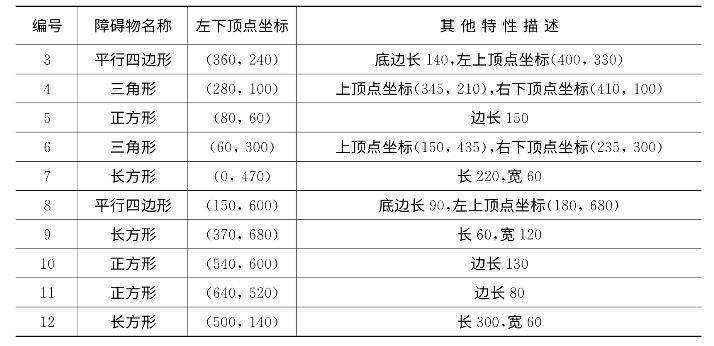
图2.1是一个800×800的平面场景图，在原点O（0，0）点处有一个机器人，它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，障碍物的数学描述见表2.1。在图2.1的平面场景中，障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过10个单位）。规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

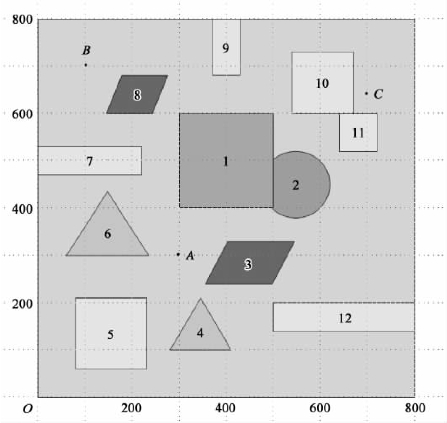
图2.1　800×800平面场景图

表2.1　障碍物的数学描述

续　表

(www.daowen.com)

机器人直线行走的最大速度为v0＝5个单位/s。机器人转弯时，最大转弯速度为v＝，其中ρ是转弯半径。如果超过该速度，机器人将发生侧翻，无法完成行走。

请建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。对场景图中4个点O（0，0），A（300，300），B（100，700），C（700，640），具体计算：

（1）机器人从O（0，0）出发，O→A、O→B、O→C和O→A→B→C→O的最短路径。

（2）机器人从O（0，0）出发，到达A的最短时间路径。

要给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间。