问题

一个冬天，某一森林不幸发生火灾，消防站接到报警后立即决定派消防队员前去救火，然而，派多少队员去呢？派的队员越多，森林的损失就越少，但救援的开支就会增加，所以需要综合考虑森林损失费和救援费与消防队员人数之间的关系，以总费用最小来决定派出队员的数目。

解题思路

森林损失费通常正比于烧毁的森林面积，而烧毁的森林面积与失火的时间、消防队员开始救火的时间、火被扑灭的时间有关，火被扑灭的时间又取决于消防队员的人数，人数越多灭火越快，救援费除与消防队员人数有关外，也与灭火时间长短有关。事实上，通过从消防部门获得的信息：救援费包括两部分，一部分是灭火器材的消耗及消防队员的薪金等，这些与消防队员人数及灭火时间均有关；另一部分是运送消防队员和器材等一次性支出，与消防队员的人数及器材的数量有关。

另外，烧毁的森林面积与火势的蔓延程度有关，而火势的蔓延程度与天气有很大的关系，如刮风、下雨等。为了便于叙述，引进一些符号：

记失火时刻为t＝0，开始救火时刻为t＝t1，火被扑灭时刻为t＝t2。设在时刻t烧毁的森林面积为B（t），则最终烧毁的森林面积为B（t2）。那么，怎样刻画火势蔓延的程度呢？可以用单位时间烧毁的森林面积来表示，即。容易知道，在消防队员到达之前，即0≤t≤t1，火势是越来越大，即随t的增大而增大；开始救火以后，即t1≤t≤t2，如果消防队员救火能力足够强，火势会越来越小，即会减小，并且当t＝t2时。

通过以上分析知道，烧毁森林的损失费、救援费以及火势蔓延程度与时间t、消防队员人数的具体关系是建立数学模型的关键问题。为了便于建模，做如下一些假设：

（1）为了简单起见，不考虑刮风、下雨等情况。

（2）假设烧毁森林的损失费与烧毁面积B（t2）成正比，比例系数为c1，c1即为烧毁单位面积的损失费。

（3）设从失火到开始救火这段时间（0≤t≤t1）内，火势蔓延程度与时间t成正比，比例系数为β，β称为火势蔓延速度。

（4）设派出消防队员x名，并且假设开始救火以后（t≥t1）火势蔓延速度降为βλx，其中λ可视为每个队员的平均灭火速度，显然应有β＜λx。

（5）设每个消防队员单位时间的费用为c2（消防队员的工资。为简单起见，把消防剂的消耗及消防器材的损耗等费用也分摊在每个消防队员身上，合并记为c2），于是每个队员的救火费用是c2（t2－t1）；设运送每个消防队员的一次性支出为c3（将运送器材的费用也分摊到每个队员身上，合并记为c3）。

第（3）条假设可做如下解释：火势以失火点为中心，以均匀速度向四周呈圆形蔓延，所以蔓延的半径r与时间t成正比。又因为烧毁的森林面积B与r2成正比，故B与t2成正比，从而与t成正比。可以看出，在不考虑天气的情况下，这个假设是合理的。

根据假设（3）、（4）可知，火势蔓延程度在0≤t≤t1内线性地增加，在t1≤t≤t2内线性地减少，记t＝t1时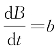，，则与时间t的关系如图1.6所示。(www.daowen.com)

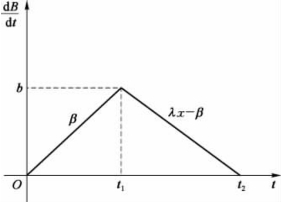
图1.6　随时间t变化的示意图

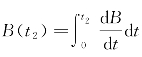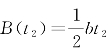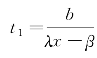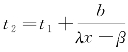烧毁的森林面积恰好就是图中三角形的面积（根据定积分的几何意义），显然。也可写出关于t的解析式代入上述积分计算可得，而t2满足t2－，即，从而可得

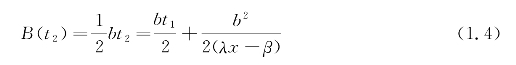
根据假设（2）、（5），森林损失费为c1B（t2），救援费为c2x（t2－t1）＋c3x。于是可得救火总费用为

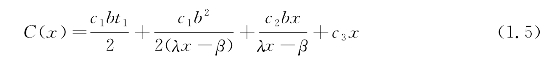
这样，问题就归结为求x使C（x）达到最小。这就是森林救火问题的数学模型。

这是一个一元函数求极值的问题。令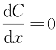，可以得到应派出的队员人数为

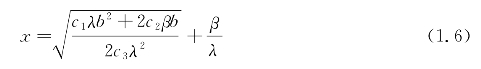
从上述结果，可以看出应派出队员人数由两部分组成，其中一部分是为了把火扑灭所必需的最低限度，因为β是火势蔓延速度，而λ是每个队员的平均灭火速度，所以这个结果是明显的。从图1.6也可以看出，只有当时，斜率为λx－β的直线才会与t轴有交点。另一部分，即在最低限度之上的人数，与问题的各个参数有关。当消防队员灭火速度λ和救援费用系数c3增大时，消防队员数减少；当火势蔓延速度β、开始救火时的火势b及损失费用系数c1增加时，消防队员数增加，这些结果与常识是一致的。另外所得结果还表明，当救援费用系数c2变大时消防队员数也增大，请读者考虑这个结果是否合理。

实际应用这个模型时，c1、c2、c3是已知常数，β、λ由森林类型、消防队员素质等因素决定，可以根据平常积累的数据预先制成表格以备查用。较难掌握的是开始救火时的火势b，不过，它可以由失火到救火的时间t1按b＝βt1算出，或根据现场情况估计。

评注建立这个模型的关键是对的假设，比较合理而又简化的假设（3）、（4）只能符合无风的情况，在风势的影响下应考虑另外的假设；再者，有人对消防队员灭火的平均速度λ是常数的假设提出异议，认为λ应与开始救火时的火势b有关，b越大λ越小，这时要对函数λ（b）做出合理的假设。再得到进一步的结果。可见这个模型改进的余地还很大，有兴趣的读者可进一步研究。