问题

椅子是大家经常用到的一件日常用品，当我们把一只椅子随手放在某处，可能没有放稳，不过，根据常识，只要地面起伏不是太大，稍微将椅子挪动几次或旋转多次（或一次）就可以放稳。那么，关于这一问题，如何用严格的数学语言来论证呢？

解题思路

首先要明确放稳的标准，通常所谓的“稳”，就是“稳定”“不倒下去”的意思，还有一种就是椅子的四条腿同时着地，显然，这两种意思是不一样的。这里，采用后一种标准，即将椅子的四条腿是否同时着地作为衡量能否放稳的标准。那么，与此相关的因素有：椅子四条腿的粗细、长短，地面的不平程度，椅子的移动情况等。为了讨论问题的方便，先做一些必要的假设：

（1）椅子四条腿粗细均匀，长度相等，椅脚与地面的接触处视为一个点，四脚的连线呈正方形。

（2）地面高度是连续变化的，沿任何方向都不会出现间断（没有像台阶那样的情况），即地面可视为数学上的连续曲面。

（3）对椅脚的间距和椅腿的长度而言，地面是相对平坦的，使椅子在任何位置至少有三条腿同时着地。

椅子在地面上移动可用旋转和平移两个变量来刻画，为简便起见，仅考虑做旋转的情况。

设椅脚的连线为正方形ABCD，对角线AC与x轴重合，当椅子绕中心点O旋转后对角线A′C′与x轴的夹角为θ（图1.5），记A′，C′两脚与地面的距离之和为f（θ），B′，D′两脚与地面的距离之和为g（θ）。由假设（2），f（θ），g（θ）都是θ的连续函数，由假设（3），对于任意的θ，f（θ）与g（θ）中至少有一个为0。不妨设g（0）＝0，f（0）≥0，于是把椅子能放稳归结为证明如下的数学命题。(www.daowen.com)

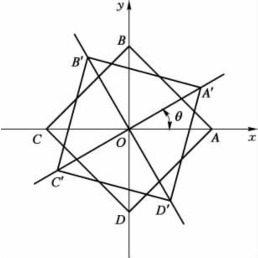
图1.5　椅脚旋转前后示意图

连续函数f（θ）及g（θ），对任意θ有f（θ）·g（θ）＝0且g（0）＝0，f（0）≥0，则存在θ0，使得f（θ0）＝g（θ0）＝0。这就是本问题的数学模型。接下来就是模型的求解过程。

（1）若f（0）＝0，则取θ0＝0，此时命题成立。

（2）若f（0）＞0，则将椅子旋转，这时对角线AC与BD互换，由g（0）＝0，f（0）＞0知。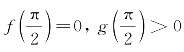

令F（θ）＝f（θ）－g（θ），则有F（0）＞0，，显然F（θ）是连续函数，由连续函数的零点存在定理可知，必存在，使F（θ0）＝0，即f（θ0）＝g（θ0），又因为f（θ）·g（θ）＝0，故有f（θ0）＝g（θ0）＝0。

由于这个实际问题非常直观、简单，模型的解释和验证就略去了。这个模型的巧妙之处在于用一元变量θ表示椅子的位置，用θ的两个函数表示椅子四脚与地面的距离。另外指出，该模型中椅子四脚连线呈正方形的假设及椅子旋转90°并不是本质的，读者可以考虑四脚连线呈长方形的情形。

可进一步思考的问题：椅子四脚连线为等腰梯形时，如何建模与求解？椅子四脚连线呈什么形状时，椅子一定能放稳（即寻找能放稳的充分必要条件）？