问题

现有一个教室长为15 m，宽为12 m，在距离地面高2.5 m的位置均匀地安放4个光源，假设横向墙壁与光源、光源与光源、光源与纵向墙壁之间的距离相等，各个光源的光照强度均为一个单位。要求：

（1）如何计算教室内距离地面1 m处任意一点处的光照强度？（光源对目标点的光照强度与该光源到目标点距离的平方成反比，与该光源的强度成正比）。

（2）画出距离地面1 m处各个点的光照强度与位置（横纵坐标）之间的函数关系曲面图，同时给出一个近似的函数关系式。

解题思路

假设光源对目标点的光照强度与该光源到目标点距离的平方成反比，并且各个光源符合独立作用与叠加原理。光源在光源点的光照强度为“一个单位”，并且空间光反射情况可以忽略不计。

取地面所在的平面为xOy平面，x轴与教室的宽边平行，y轴与教室的长边平行，坐标原点在地面的中心，如图1.1所示。在空间中任意取一点i，它的坐标可以表示为（xi，yi，zi），那么空间点i的光照强度Ei应该满足以下公式：

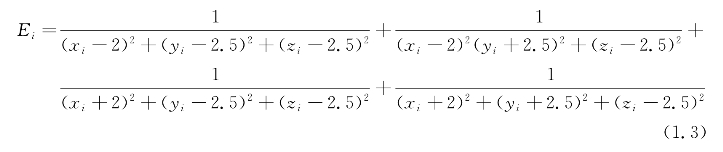
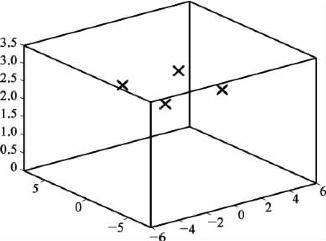
图1.1　教室坐标示意图(www.daowen.com)

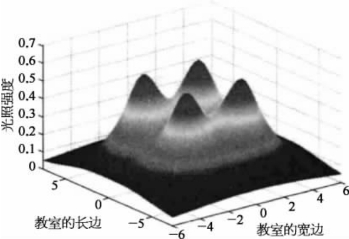
图1.2　无反射情况下教室光照示意图

将空间点i的纵坐标设定为1，就可以计算距离地面高1 m处各点的光照强度。在MATLAB计算中都是对离散点进行计算操作，因此将距离地面高1 m处的12 m×15 m平面离散为网格，每隔0.25 m取一个点，而点与点之间采用插值算法可以得到这个平面的光照强度，如图1.2所示。

通过示意图可以发现，在这个距离地面为1 m的平面中，四个灯下的光照强度最强。上述模型是建立在不考虑墙面反射基础上。那么，忽略反射的想法是否正确呢？考虑墙面反射对于平面各点光照强度会带来怎样的影响？为方便求解，首先假设墙面反射满足镜面反射原理，这也是最简单的假设。重新计算可以得到在距离地面为1 m的平面中各点的光照强度如图1.3所示。对比有无一次镜面反射，平面光照强度的改善情况如图1.4所示。从图中可以发现：墙边附近的光照强度改善最大，墙角和墙边的改善最小。因为墙角和墙边的反射最少，这些都与实际情况符合。

图1.4显示，通过一次镜面反射光照强度最大可以提高0.1左右。那么如果考虑二次反射，二次反射所能增加的光照强度将更加小，可以忽略不计。需要注意的是：在实际生活中，墙面的反射并不是简单的镜面反射，光源也不是点光源，光照强度也并非简单叠加。这样建立的模型将更为复杂。

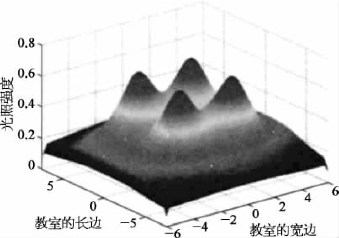
图1.3　反射情况下教室光照强度示意图

图1.4　两种情况下教室光照强度对比示意图