MOOC 2.6　方程组的误差分析

解线性方程组的直接法产生误差的主要原因：①不同的算法及舍入误差的影响；②方程组本身固有的问题（病态或良态）.前面分析了方程组直接法的不同算法，本节将分析方程组的状态并估计算法的误差，即原始数据扰动对解的影响.

考虑n阶线性方程组Ax=b，其中A为非奇异矩阵.

由于A（或b）的数值是测量得到的，或者是计算的结果，在第一种情况下A（或b）常带有某些观测误差，在后一种情况A（或b）又包含有舍入误差.因此我们处理的实际矩阵是A+δA（或b+δb），下面我们来研究数据A（或b）的微小误差对解的影响.首先考虑一个例子.

设方程组Ax=b，即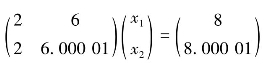，它的精确解为（1，1）T.

现在考虑系数矩阵和右端项的微小变化对方程组解的影响，即考查方程组

其解变为（10，-2）T.扰动后方程组的解面目全非了，真所谓“差之毫厘，谬以千里”，这种现象的出现完全是由方程组的性态决定的.

利用Matlab函数解线性方程组，输入

a=［2 6；2 6.00001］；b=［8，8.00001］'；x=a\b得到解：(www.daowen.com)

x=1　1

输入

a=［2 6；2 5.99999］；b=［8，8.00002］'；y=a\b

得到解：

y=10　-2

定义6　如果矩阵A或常数项b的微小变化，引起方程组Ax=b解的巨大变化，则称此方程组为病态方程组，矩阵A称为病态矩阵（相对于方程组而言），否则称方程组为良态方程组，矩阵A称为良态矩阵.

我们需要一种能刻划矩阵和方程组“病态”程度的标准.