数值计算中首先要分清问题是否病态和算法是否数值稳定，计算时还应尽量避免误差危害，防止有效数字的损失，下面给出若干原则.

1）避免两相近的数相减

在数值计算中两相近数相减有效数字会严重损失.

例1-2　计算1-cos 2°（用4位有效数字表示三角函数值）.

解

具有4位有效数字的近似数0.999 4经过运算后，只有1位有效数字.

例1-2说明必须尽量避免出现这类运算，最好是改变计算方法，防止这种现象产生.对于例1-2，若利用三角恒等式进行公式变换，则

秦九韶算法　秦九韶算法是我国宋代的一位数学家秦九韶提出的.国外文献通常称这种算法为霍纳算法，其实霍纳的工作比秦九韶晚了5个多世纪.

秦九韶（1202—1261），字道古，四川安岳人，中国南宋数学家，1247年写成《数书九章》.

例1-3　用克莱姆法则求解线性方程组Ax=b.

解　用克莱姆法则求解n阶线性方程组，当n=20时，需要计算21个20阶行列式.按行列式定义计算，每个行列式需要计算（20-1）×20！次乘法，如果加减运算的计算次数忽略不计，则总的计算量约为21×19×20！.假设计算机每秒可作1亿次乘除运算，则求解这样一个线性方程组需用的时间是多少？

利用Matlab程序计算如下：

程序运行，得到需用的时间约为307 816年.

天啊，30多万年的时间！(www.daowen.com)

如果改用第2章的高斯消去法只需2 000多次乘除运算，并且n越大2种算法的计算量差别越大.这说明将一个数学模型转化为计算机程序时，对算法的研究十分重要.

注　一个算法的计算代价就是完成计算需要支付的金额.算法由算术运算组成，用计算机来实现.计算机计费的主要依据：一是使用中央处理器（CPU）的时间，主要由算术运算的次数决定；二是占用存储器的空间，主要由使用数据的数量决定.

算法的计算代价称为算法的复杂度，其中，算法的计算量称为时间复杂度；算法需占用存储空间的量度称为空间复杂度.

3）要避免用绝对值很小的数作除数

避免用绝对值较小数作除数的方程组示例

用绝对值很小的数作除数，舍入误差会增大，甚至会在计算机中造成“溢出”错误.如计算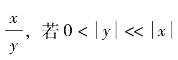，则可能对计算结果带来严重影响，使数值不稳定，应尽量避免.

又如，计算，当x＞＞0时，分母的绝对值很小，此算法是数值不稳定的.

4）两数相加要防止大数“吃”掉小数

在数值运算中参加运算的数有时数量级相差很大，而计算机位数有限，如不注意运算次序就可能出现大数“吃掉”小数的现象，影响计算结果的可靠性.

例如，在5位十进制计算机上，计算12 346+0.6+0.6-12 345.

将运算的数写成规格化形式，在计算机内运算时要对阶，因此

结果显然不可靠，这是由于运算中出现了大数12 346“吃掉”小数0.6.

因此，应合理安排运算顺序，防止参与运算的数在数量级相差悬殊时，大数“淹没”小数的现象发生.多个数相加时，最好从其中绝对值最小的数到绝对值最大的数依次相加；多个数相乘时，最好从其中有效位数最多的数到有效位数最少的数依次相乘.