ElGamal 密码体制的安全性是基于求解离散对数问题的困难性。 ElGamal 密码体制是非确定性的， 因为每次加密都要选择一个随机数， 相同的明文随着加密前随机数的不同而产生不同的密文。

ElGamal 密码体制既可以用于加密， 也可以用于签名， 其安全性依赖于有限域上计算离散对数的难度。

1. ElGamal 密码体制的算法描述

1) 密钥产生

要产生一对密钥， 首先选择一个素数p、 整数模p 的一个原根g， 并随机选取x， g 和x都小于p； 然后计算:

公开密钥是y、 g、 p， g、 p 可以为一组用户共享； 私有密钥是x。

2) ElGamal 加密算法

将明文信息M 表示成{0，1，…，p-1} 内的数。 秘密选择随机数k， 计算:

将C=(a，b)作为密文。

3) ElGamal 解密算法

设密文为C=(a，b)， 则明文为

验证: ax≡gkx mod p， b/ax≡ykM/ax≡gxkM/gxk≡M mod p

2. ElGamal 密码体制实例

1) 生成密钥

A 选取素数p=2357 及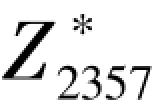， 生成g=2， A 选取私钥x=1751 并计算:

A 的公钥是p=2357、 g=2、 gx =1185。

2) 加密

为加密信息m=2035， B 选取一个随机整数k=1520， 并计算:

B 发送a、 b 给A。

3) 解密

A 计算:

3. ElGamal 数字签名(www.daowen.com)

ElGamal 数字签名主要利用离散对数的特性来实现。 其具体方式如下:

(1) 选择一个大素数P、 一个本原元g、 一个随机整数d， d∈[2，p-2]。

(2) 生成β， β=gd mod P。

(3) 此时P、 g、 β 就是公钥， 记作Kpub。

(4) ElGamal 数字签名记作sig(x，k) =(r，s)； x 是明文的摘要， k 是临时私钥的随机值，记作Kpr， r、 s 是构成签名的两个整数。

(5) 签名生成: r=gk mod P； s=(x-dr)k -1 mod (p-1)。

(6) 生成签名后， 签名随明文一起发送给接收方。

(7) 接收者收到消息后， 计算t≡βrrsmod P。

(8) 验证: 若t≡gx mod P， 则该签名有效， 数据未被窜改； 反之， 该签名无效。

例2 -1　B 发消息给A， 对消息使用ElGamal 数字签名。

(1) B 选择素数P=29、 本原元g =2、 随机整数d =12、 临时私钥k =5、 明文的摘要x=26。

(2) 由公钥β=gd mod P 可知， β=4096 mod 29， 即β=7。

(3) B 将公钥(P=29， g=2， β=7) 发给A。

(4) 计算签名。 由r=gk mod P 可知， r=25 mod 29， 即r=3。

计算签名后， 将r=3、 s=26、 x=26 发送给A。

(5) A 收到消息后， 验证签名:

验证成功。

4. ElGamal 加密算法安全性

攻击ElGamal 加密算法等价于解离散对数问题， 这个求解问题是比较困难的。 所以， 针对ElGamal 加密算法的攻击会通过其他路径来实现。 在实现ElGamal 加密算法过程中， 应使用不同的随机数k 来加密不同的信息， 否则会带来新的安全问题。 例如:

假设用同一个k 加密两个消息m1、 m2， 所得到的密文分别为(a1，b1)、(a2，b2)， 则b1/b2 =m1/m2， 故只要已知m1， 就可以很容易地计算m2。