离子键指阴离子、阳离子间通过静电作用形成的化学键，通过两个或多个原子，或者化学集团失去或获得电子而成为离子后形成。带相反电荷的离子之间存在静电作用，当两个带相反电荷的离子靠近时，表现为相互吸引，而电子和电子、原子核与原子核之间又存在着静电排斥作用，当静电吸引与静电排斥作用达到平衡时，便形成离子键。因此，离子键是阳离子和阴离子之间由于静电作用所形成的化学键。此类化学键往往在金属与非金属间形成。失去电子的往往是金属元素的原子，而获得电子的往往是非金属元素的原子。通常，活泼金属与活泼非金属形成离子键，如钾、钠、钙等金属和氯、溴等非金属化合时，都能形成离子键。

离子键是由电子转移（失去电子者为阳离子，获得电子者为阴离子）形成的，即正离子和负离子之间由于静电引力所形成的化学键。离子既可以是单离子，如Na﹢，Cl﹣；也可以由原子团形成，如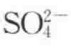，等。研究认为，在分子或晶体中的原子并不是简单地堆砌在一起，而是存在着强烈的相互作用。化学上把这种分子或晶体中原子间（有时原子得失电子转变成离子）的强烈作用力叫作化学键。键的实质是一种力，所以有的又叫键力，或就叫键。以钠与氯化合生成氯化钠为例：从原子结构看，钠原子最外电子层上有1个电子，容易失去；氯原子在外电子层有7个电子容易得到1个电子。当钠原子与氯原子相遇时，钠原子失去最外层的一个电子，成为钠离子，带正电，氯原子得到钠失去的电子，成为带负电的氯离子，阴阳离子的异性电荷的吸引作用，与原子核之间、电子之间的排斥作用达到平衡，形成了稳定的离子键。

离子键的作用力强，无饱和性，无方向性。离子键存在于离子化合物中，离子化合物在室温下是以晶体形式存在。离子键较氢键强，其强度与共价键接近。离子键的键能比较大，反映在离子化合物中就是高熔沸点，离子键的键能被称作晶格能，晶格能的符号与离子晶体解离过程焓变的符号保持一致。晶格能可以通过玻恩-哈勃循环（Bōrn-Haber cycle）或玻恩-兰德公式（Bōrn-Landé）计算得出，也可以通过实验测量。

以含羧基的胶剂为例，在粘接金属时，可能与金属表面上的氧化膜Me﹢O﹣有下列反应：

如果不慎使玻璃瓶口与玻璃塞之间碰到含Ca（OH）2的溶液，也会引起离子键型的粘接，即

在离子型化合物中，正、负离子间的相互吸引力为

式中，Q1，Q2分别为正负离子所带的电量；R为正、负离子间的距离。当距离足够小时，由于正、负离子内的电子云靠近而开始产生斥力作用。若正、负离子处于一定距离而使以上两力达到平衡时，即引力与斥力大小相等，则体系的势能最低。引力与斥力大小相等，则体系的势能最低。如果正、负离子间距离被拉伸到比平衡时的大，合力随距离的增加会达到一极大值，然后逐渐减少，最后趋近于零。外力将组成分子的离子（或原子）推到无穷远所需做的功为D，它是该化学键的解离能或称键能，一般常用D值表征结合力。

倘若要估算结合力的大小，可以从常态晶体化合物的讨论开始。假如以氯化钠离子晶格为例，它是立方点阵，每一个离子都有6个和其电荷相反的相邻离子配位，即在NaCl点阵中的配位数是6。稍远一点，与中心离子相距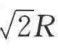处，有12个带相同电荷的离子。再远一点就是8个带相反电荷的离子，中心离子与它们的距离是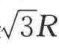等。因此一个离子和它周围离子间的静电相互作用可以表示为

式中，A为Madelung常数。

对配位数为6的NaCl晶体来说

由正、负离子电子云所引起的斥力势能，同样也可以表示为紧邻离子间距离的函数。因为它只在短距离内起作用，且随着距离的增大而迅速地减弱，于是能以B/Rn表示。其中B和n都是常数，n称Bōrn指数，在一般情况下为5～12之间，但随离子中电子个数的增多而增大。

在NaCl中，Na﹢的电子层结构与Ne类同，n Na﹢＝7，而C1﹣的电子层结构类同于Ar， ncl﹣＝9，因此，Na Cl的n取平均值为8，于是NaCl点阵的总势能（Na﹢和C1﹣的带电荷数Z﹢和Z_都等于1）可以表示为

B可以由平衡状态的U为极小值时确定，即将U对R微分，且令其导数为零。

此式的n值可由晶体的压缩系数求得，R0是从X射线谱和电子光谱求得。按上式求得NaCl的离子晶体的点阵能（又称晶格能，是总势能的负值）为753kJ/mol。(www.daowen.com)

由式（7-26）对R微分，可求得离子间作用力F与离子间距离R的关系，即

当F达到极大值时，则R＝R1，因此

将式（7-28）代入式（7-27），得

从式（7-25）和式（7-28）可知：

由此而得：

于是

如将式（7-26）变为

则式（7-31）也可变为

上述推导所得公式是有关离子晶体（电荷数1-1型）点阵的势能和最大作用力的理论计算式。

根据以上的推导方法，对于游离的气体离子型分子，例如Na﹢Cl﹣，由于只有两个相邻的异电性离子，则Madelung常数A应等于1，其势能为

其中理论上导出的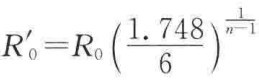，则

由式（7-33）和式（7-35）算出的NaCl游离气体型分子的键能U′0为513.5kJ/mol。要使两离子分离所需的最大力FR′＝R′1＝2.085×10﹣9N。