当结构或组分不同的两个固相相互接触形成界面时，界面处原子排列混乱而使单位面积的自由焓在扩大的界面区域的变化称为界面自由焓。实际上，在一个固体中常存在多晶结构，而由各种不同晶核取向长大的晶粒可以产生多种的接触界面，即不同的晶面彼此或与某些非晶体之间的接触界面。这种固-固界面自由焓比两个不同固相之间的接触界面自由焓更难予以实验测定。

从热力学可知，界面能是一种对比固相本体内能的超量，所以都是正值，势必会自发地向降低体系总能量的方向移动。因此，固体内部的界面越多就越不稳定。一般规律是固体的单相单晶结构比多晶结构的稳定，而单晶结构的多面体各晶面是以表面自由能最小原则组合的为最稳定。当固体形成时，由于晶核的产生和晶粒长大以及固体内基本粒子移动极其困难等动力学因素，实际上很可能会使一个各向异性的晶体以多晶结构组成固相。固体的界面分两类，一是同相界面，包括晶界、孪晶界、畴界和堆垛层错等；二是异相界面，即结构不同两相晶粒之间的分界面。根据晶界两侧晶粒取向差的大小，晶界又分为小角晶界和大角晶界。

Fowler和Guggenheim使用Lennard-Jones势估算了两边无穷固相的比界面自由焓为

式中，A12为分子间色散作用能常数，那么它就可以通过极化率α和电子振动频率v求得，即

对于相同分子的极化率，则此式变为

图7-1 I相和J相间作用势能是一层层平面模型

图7-2 假定J相的分子作用势能是均匀连续模型

由于上式的处理是将两相固体视为分子极化率均匀分布的连续体，而事实上固体的分子极化率是以单个分子为中心的、非连续对称分布的，因此两固相的距离越接近分子尺度，以积分求黏附能总和的结果越偏低。

Fowkes提出了部分修正的计算界面能方法。他认为界面的色散相互作用都是由均匀地富集在与界面平行的一层层平面上的分子色散产生的，那么离开J相表面距离为dij的I相内，其中i层分子与J相相互作用的示意可见图7-1。若仍然假定J相的分子作用势能是均匀连续的（见图7-2），且能以Lennard-Jones方程来描述，其斥力可暂时忽略不计，则一个i分子与J相的相互作用势能为

对比上述的均匀连续模型可知，分子i与J相中相距R、厚度为△、分子密度为njdj/△（其中dj是J相中各平面层间距）的某一平面j之间的相互作用势能是：

当△/R很小时，上式可以简化为

由上可知，分子i对J相中所有平面层的相互作用势能只能用加和法求得，即

现R＝dij，如果又等于dj，则式（7-7）可以变成

当j从0加和至1 000时，其值约为1.082。由于上述的推导仅考虑了引力项，若还需斥力项，有时可以采用校正因子fij相乘方法，即

于是在两相间隔dij的I相各层中，其第一层与J相所有各层分子间的相互作用势能应该是：(www.daowen.com)

式中，nidi相当于I相中层间距为dj的各层上单位面积的分子数。然后，对I相各层的作用势能逐层加和，即

对于I相与J相层间距和界面距全部相等为d的特殊情况，则

当i＞105时，上式就成为

如果I与J为同一相，则

上述式中若有校正因子fij与fj，其数值在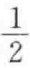～1之间，一般取。

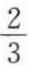若Fowler和Guggenheim所提出的方法，也先忽略了分子间的斥力，然后采用校正因子，则所得结果为

将式（7-14）与式（7-15）比较，显然前式的估算值比后者的大许多倍。

由于单位面积上的表面总能量超量与比表面自由能之间相差了熵项，即

E－v＝TS 　（7-16）

对此可以采用Hoersch Meyer的建议，使用比例因子w让v与E1联系，即

所以

例如，20℃时正八烷的w＝0.87，ni＝3.1×1028CH2或CH3原子团/m3，αi＝2.12×10﹣30m3，di＝4.6×10﹣10m，fi＝0.9和hv近似等于电离能约为10.55eV（即1.68×10﹣18J），由此所估算的比表面自由能vi值为18.9×10﹣3J/m2，这与测定值21.8×10﹣3J/M2相近。

由此得知，根据式（7-18）的计算所得之近似结果，可以作为对界面能的评估。上例正八烷的w＝0.87，但对于表面能较高的固体，w接近于1。