当三维空间活动的气体被固体吸附剂单层物理吸附在表面上时，该气体就丧失了一个自由度而成为二维活动状态。所以，此时可以应用界面二维状态方程来描述。在气相与凝聚相接触的体系中，可以将其分成α与β两个体相及表面相σ等三部分。当建立吸附平衡时，体系的自由能为

G＝Gα＋Gβ＋Gσ＝Gα，β＋Gσ　（6-65）

根据热力学基本公式：G＝f（T，p，n1，n2，⋯） 　（6- 66）

假如体系自由能发生微量变化，则

表面相上的Vσdp与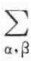Vdp比较可以不予考虑，但表面相所表现的二维体系表面功ГdA必须给予考虑。如果体系从始态按原比例增加各组分的量到n1，n2，n3，⋯的终态，而

μi和Г均不会变化。那么，对式（6-67）积分即可得

若在同样的始态到终态的等温变化过程中不按原组成比例增加，则

在等温条件下，取其中表面相的

比较上述两式，可以得到Gibbs-Duhem方程在表面上的应用公式，即

设单纯是气体吸附质2吸附在固体1表面上，则

式中，Г2为固体1单位表面积上的吸附量，而此吸附气体化学势及其压力的关系可用理想气体热力学化学势公式表示，则(www.daowen.com)

因此

式中，表面积A等于比表面积ASP乘以吸附剂重量。对于某一给定的吸附剂则其ASP不变，但恒温下的不同p值其吸附平衡量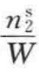也不同。将上式积分，即

式中，Г0为纯净吸附剂表面张力；Γ为铺有单分子层吸附质的吸附剂表面张力；π为表面膜压力或二维表面空间压力。

通常的气-固物理吸附平衡可用下式表示：

这是Henry定律在表面吸附上的应用，即一定温度和低压下的吸附量与气体压力呈直线关系，比例常数C是Henry吸附平衡常数。于是式（6-77）成为：

式中，ASPW/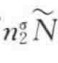＝A，为每个分子所占的表面积，则

πA＝kT　（6-79）

这就是表面相中表面吸附二维理想气体方程。如果需要二维空间压力π化为三维空间压力p时，可将π除以表面吸附膜厚度δ，即一般是

例如，有一厚度δ为10﹣9m数量级的表面膜，当π值约为10﹣3N/m2时寸，p＝107Pa，其值接近100atm。在如此高的压力下，表面相中的吸附质就不再服从上述理想气体方程。这与采用三维空间理想气体方程的修正方法一样，可以做面积的修正，即用（S－S0）代替S，S0是吸附分子的真正面积，则π（A－A0）＝k T，可得范德瓦尔斯真实气体状态方程为

式中，b＝S0，与引力修正项a都是二维常数。因此，该式称为范德瓦尔斯型二维状态方程。