理论近似计算表面能，因所考虑的固体种类不同而异。但大体上是分为两步进行。第一步，靠断键将固体劈开分成两部分，从而产生表面。但此时表面原子仍固定在原来处于体相时的位置，由此得到对表面能的主要贡献。第二步，表面原子在垂直表面的方向移动，借以达到它的新的平衡位置，能量减少，由此可得表面能。固体表面能的理论计算和固体的力学性质有关，需要对分子间作用力做更详细的探讨。对不同类型的固体，其表面能的理论估算方法也不同，现在分别做如下讨论。

1.共价键晶体

最简单的共价键晶体，其晶格结点上均由σ-共价键连接的原子所占据。因此，只要考虑邻近原子对间的相互作用，不需要考虑长程相互作用。Harkins认为，要将横截面为单位面积的晶体一分为二，必须对抗分子间作用力而做功，其数值是表面能的2倍。横截面的表面能是将连接单位面积上原子的所有键打断所需能量的一半，即

式中，E内聚表示单位面积上原子与对应平行截面连接的所有键的键能之和。由于在计算中忽略了表面扭变，导致这些近似的计算值往往不太符合实际情况。

2.金属键晶体

对于具有金属键的材料，可以通过其升华能来计算表面能。以金属键结合的原子晶格，只需考虑与其相邻配位原子的键合。假如升华一个原子破坏了上述的键合，而破坏过程中所需的键能是以升华热表现出来。那么，形成单位面积新表面时，上层与下层的键合势必破坏。由此可知，表面张力Γ与键能的关系十分密切，且与其升华热也有内在的联系。对于金属，最好将表面能作为由于表面的存在而引起自由电子动能的变化来考虑。例如，一个完美纯金属原子的面心立方晶格，其中的每一个本体相原子应具有12个最近邻之配位原子（Z＝12），而密度最高之晶面（111）表面约一个原子上层，它所空缺的原子有三个，一个原子从固体本体相向蒸气相转移所吸收的能量，即破坏12根键所需的键能；当形成（111）表面时，裸露第一个原子其表面要移去三个原子，即断裂了三根键，裸露该原子后，每再裸露一个原子仅移去其上两个原子。由此统计而估算摩尔表面自由能

即摩尔表面自由能等于比表面自由能（J/M2）乘以摩尔面积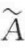（m2/mol）。此公式与自金属实验数据得到的实验关系式为

显然前者的系数稍大了一些，如果做进一步处理，可以得到与实验关系式相同的系数。

例如，铜的摩尔升华热升＝317262J/mol，由铜的单位面心晶格边长3.6×10﹣10m和（111）面计算，裸露在表面上的原子数为1.78×1019/m2，则Гm＝0.16×317 262＝50 761.92（J/mol），根据式（6-13）计算可得Г为1.5J/m2。

3.离子晶体

离子晶格是离子间主要以库仑力相互作用而键合起来的，不能只考虑一对正负离子间的关系。晶格不太复杂时，可将离子间的相互作用加和。以NaCl晶体为例，指定一钠离子所受的力应是最靠近的一个氯离子对它的静电吸引力，再加相隔此氯离子的另一钠离子对它的静电斥力，又加上该钠离子旁边的第二个氯离子对它的吸引力，这样逐个计算至超过库仑力的作用范围为止。这种计算表面能的方法，如果还考虑偶极相互作用力，显然更为复杂了。因此，设想将此库仑引力等视为离子键晶体表面的应力。若将此晶体拉开则产生了两个单位面积新表面，如图6-9所示，那么，这一拉力所做的功正好等于新生表面的比表面自由能，它相当于2Г，即2Г＝ʃfdr按照图6-10所示的作用力随距离变化曲线那样，假定应力f随两单位面积新表面相隔的距离变化可以采用正弦曲线来处理，则

图6-9 离子晶体两新表面间的位能曲线

图6-10 离子晶体两新表面间作用力随距离变化曲线

如图6-9所示，当两个新表面相隔为平衡距离r0时，其应力为零；当r＞r0时，应力逐渐增加，达到最大值后又逐渐降低；若r＝2r0时，f再次为零。而r＞2r0时的f仍趋于零，表明正弦曲线公式不适用。在平衡距离r0处，正弦曲线的曲率应等于零，表现出其线弹性，于是可以应用弹性模量

则

E可从力学所测定的数据中得到，r0是通过X射线测试数据求得的。现将某些离子晶体的比表面自由能理论计算值与实验值分别列于表6-1中，以便于进行比较。

表6-1 几种离子晶体理论计算和实测的比表面自由能值

4.分子晶体

对于以较长程的范德瓦尔斯力内聚的分子晶体，其理论处理是困难的，必须考虑表面扭变而分子重新定向问题。其一最简单的特例是稀有气体的单原子分子晶体，它不存在分子取向问题，因此其表面能的计算困难最小。倘若将它们的面心立方晶格视为每隔一个晶格空了一个位置的简单立方晶格，其表面能主要是近表面的分子过剩势能，因此需要计算跨越横截平面的净相互作用能。(www.daowen.com)

假设某材料的圆柱体被切为具有单位面积切面的平面，如图6-11所示，要使此圆柱体一分为二，必须对抗分子间作用力而做功，其数值是表面能的2倍。两个分子的相互作用能可用Lennard-Jones势能函数表示：

图6-11 界面上的分子间作用力

式中，A为引力常数；B为斥力常数；r为分子间距离。引力常数和斥力常数是彼此相关的，分子间作用力为

式中，不同原子间A，B有不同取值。

设分子的密度n1是均匀的，不受其位置的影响，则图6-11中阴影部分环形体总分子数目为M，则有

M＝2πrsinθ（dr/sinθ）n1df 　（6-23）

在图6-11中x点上的一个分子受到环形体全部分子在z方向上的作用力为

在宽度为df的环形体全部分子的作用力为

由左边整块的分子作用于x点处的分子作用力为

左边整块所有分子和右边整块所有分子的总作用力Ft为

式中，a是左、右两块表面的距离，即

如两个表面是将材料分离成左边和右边两块而形成的，如图6-11所示，则原来切面上每单位面积所做的功应等于此表面能的2倍，因为生成了两个表面，所以表面能应为

其中，r11是两平面间的等距离，下角标“11”表示形成的两个表面的相是同一类。因此有

但是，如r11是两个半无限长物体的等距离，则两个半无限长物体的净作用力应当是零。因此，总作用力Ft中a＝r11的条件下：

代入式（6-30）中，有

事实上，式（6-32）并不是十分精确的，因为它假设表面和本体内部结构是保持恒定的，而真实的表面结构和本体结构有差别。另外，在使一个整体分离成两个表面时，会受到力的作用，而可能发生结构的变化（如表面扭变的影响），在上述推导时，这些都没有考虑进去。

关于固体表面能和表面自由能的理论计算，由于某些理论处理十分困难或者计算非常烦琐，致使许多固体的表面能不可能直接计算。即使有的可以进行理论计算，所得的理论值并不一定理想，它们与实际值往往有很大的差异。甚至从实验测定中得到的数据，也由于固体的形成过程或晶面等不同，造成所得的值不尽相同。但是固体表面能的理论计算作为实验结果的参考值还是非常需要的。