液-液界面张力虽然可以通过实验进行测定,但人们更希望了解它与两液体表面张力之间是否存在某种规律性。如果能建立界面张力与纯液体表面张力之间的函数关系,就可轻松地估算任意两种液体形成的液-液界面张力。与气-液界面相比,液-液界面相中的分子聚集状态发生了明显的变化,因此两相间的界面自由焓亦必然发生变化。液-液界面自由焓来自分子间作用力,而不同液体间起主导作用的分子间作用力的形式略有不同。界面张力理论模型的物理基础就是分子间作用力,下面介绍几种界面张力理论模型。
1.Antonoff规则
Antonoff首先提出一个简单的规则:两种相互饱和的液体间的界面张力Г12等于两个液体表面张力之差,称为Antonoff规则,即
式中,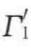 为液体1(其中含有少量液体2)的表面张力;
为液体1(其中含有少量液体2)的表面张力; 为液体2(其中含有少量液体1)的表面张力。
为液体2(其中含有少量液体1)的表面张力。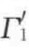 和
和 不同于Г1和Г2。例如水-苯界面,常温下20℃,Г1为72.8mN/m,
不同于Г1和Г2。例如水-苯界面,常温下20℃,Г1为72.8mN/m, 为62.1mN/m,Г2和
为62.1mN/m,Г2和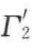 分别为28.3mN/m和28.2mN/m。
分别为28.3mN/m和28.2mN/m。
表3-2列出了一些水-液界面的相关数据,由表中的数据可以看出,Antonoff规则对一些体系适用,但并不普遍适用。
表3-2 水-液界面的相关数据参数
2.Good-Girifalco理论模型
Good和Girifalco从自黏过程的黏附功出发,对界面张力与相关液体表面张力之间的关系进行了研究。液-液界面的黏附功与两液体表面张力及界面张力的关系由式(3-13c)表达,若两液体完全一样,则称为自黏过程,自黏功Wc可表达为
Wc=2Г1 (3-3)
Good和Girifalco认为,无论是自黏功还是黏附功,都是分子间作用力变化的度量,由于范德瓦尔斯方程中两种分子引力常数与同种分子引力常数间存在几何平均的假设,在非电解质溶液理论中取得成功,他们设定,对于黏附功有:
结合式(3-3)和式(3-13c)(参见3.2节中此式),可得
上式称为Good-Girifalco模型。由此可根据两种液体的表面张力推算出它们之间的界面张力。实验结果表明,对于碳氟油与碳氢油组成的液-液界面,该模型的计算值与实验值相符。但对于有机化合物与水的界面,则误差较大。这是由于两种分子体积不同和分子间作用力的性质不同,而导致几何平均规则失效。为此,可加一校正项,得
式中,φ为校正系数,其表达式参见相关文献。但这一改进意义不大,应用中仍有较大误差。
3.Fowkes模型(https://www.daowen.com)
为了解决水-液界面张力的理论估算问题,Fowkes另辟蹊径对Good-Girifalco模型进行了改进。他认为存在于分子间的各种相互作用,包括色散力、氢键、金属键以及π电子、离子之间的相互作用等,均对液体的表面张力做出贡献。但归纳起来主要有两种,范德瓦尔斯力和特殊键力,其中后者包括氢键力和金属键力。非极性液体(如饱和烃)不存在永久偶极,其自身分子间以及与其他分子之间只有色散力;极性分子(如水)间除色散力之外,还有偶极力;而金属(如水银)除色散力外,还有金属键力。总的分子间作用力是各种形式分子间作用力的代数和,表面张力也有类似性质,如水的表面张力是色散力产生的表面张力(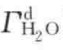 )和偶极力产生的表面张力(
)和偶极力产生的表面张力(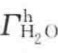 )之加和;同样地,水银的表面张力为色散力产生的表面张力
)之加和;同样地,水银的表面张力为色散力产生的表面张力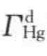 和金属键产生的表面张力Г之和,即
和金属键产生的表面张力Г之和,即
而对于非极性分子烃,只有色散力的贡献,即
因此,实验测得的烃的表面张力就是其色散表面张力。
色散表面张力是一个非常重要的物理量,通过它可以求得界面张力等物理量。当水与饱和烃接触时,其分子间作用力如图3-2所示。设水与饱和烃的表面张力分别为Γ1和Г2,两者接触后液-液界面取代了气-液界面,水-烃界面分子间的相互作用引起表面张力Г1和Г2的下降,下降值为两者分子间的色散力表面张力之几何平均值,即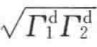 ,结合图3-2可知,当增加单位相界面时,将水分子提升至相界面所需做的功W1为
,结合图3-2可知,当增加单位相界面时,将水分子提升至相界面所需做的功W1为
同样地,将烃分子拉入相界面所需的功W2为
图3-2 水烃界面分子间作用力示意图
因此,形成该液-液界面所需的总功为(W1+W2),即界面张力Г12为
该式称为Fowkes模型。应用该模型估算液-液界面张力时须先求出各液体的Гd。对于非极性液体,实验测得的表面张力就是它的Гd。因此,只需测定极性液体和非极性液体各自的表面张力及它们之间的界面张力,便可利用式(3-9)推算出极性液体的表面张力色散成分Гd。例如,通过测定纯水和饱和烃的表面张力及水-烃界面的界面张力(Г1,Г2,Г12),则有
将式(3-10)代入式(3-9)得
式中,唯一未知的量为 ,求解该式可得
,求解该式可得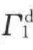 ,然后代入式(3-10a)可计算出
,然后代入式(3-10a)可计算出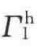 的值。
的值。
如果将饱和烃与水银形成液-液界面,用同样的办法可求得水银的色散表面张力 和金属键表面张力
和金属键表面张力 。结果表明,从10种烃-汞体系得到的汞的Γd平均值为(200±7)mN/m;从8种烃-水体系得到的水的Гd平均值是(21.8±0.7)mN/m。两组数据的相对误差均在3.5%以内,这表明Fowkes模型对水-液界面张力的估算相当成功。
。结果表明,从10种烃-汞体系得到的汞的Γd平均值为(200±7)mN/m;从8种烃-水体系得到的水的Гd平均值是(21.8±0.7)mN/m。两组数据的相对误差均在3.5%以内,这表明Fowkes模型对水-液界面张力的估算相当成功。
如果液体1和液体2的分子之间只存在色散力,则式(3-9)可简化成:
由量子力学可以导出,色散力与分子间距离的7次方成反比,若将分子近似为球状,且半径为2×10﹣10m,则相邻两分子之间的作用力与(2+2)7成反比,相间两分子间的作用力与(2+4+2)7成反比,显然后者只是前者的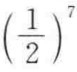 ,由此可见,“分子间力的作用范围最多只有几个分子厚度”的说法是有依据的。
,由此可见,“分子间力的作用范围最多只有几个分子厚度”的说法是有依据的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








