在一定温度和压力下，纯液体的饱和蒸气压也是一定的，但这只是针对平液面而言，而曲液面由于附加压力的作用，不同曲率的曲面包裹的液体所处的实际物理状态各不相同，因此液体的性质将随液面形状有所变化，液体的蒸气压特性就是其中的代表之一。

实验表明，微小液滴上的饱和蒸气压明显高于平液面上的饱和蒸气压。蒸气压与曲率的关系，可通过计算微量液体从平面转移到液滴的过程中吉布斯自由能的变化而获得。

设物质的量为dn的液体，从平液面转移到半径为r的小液滴表面上时，使小液滴的半径增加dr，相应地表面积增加了8πrdr，则表面自由焓的增量为Г8πrdr。另外，在这一过程中，物质的量为dn的液体从蒸气压为p0的平液面转移到蒸气压为pr的液滴，其自由焓的增加值为（dn）RT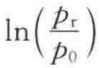，于是有

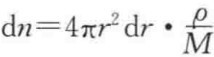由于，故(www.daowen.com)

式中，Vm为液体的摩尔体积。

式（2-20）称为开尔文方程。该式表明，在一定的温度下，液滴直径越小，所对应的饱和蒸气压越大，当r为10﹣9m时，其饱和蒸气压几乎为正常液面的3倍。对于凹液面（如气泡），由于半径为负值，气泡内的蒸气压反而小于正常液面的蒸气压。

运用开尔文方程可以解释很多界面现象，例如，毛细管内某液体若能润湿管壁，管内液面将呈凹液面，在某温度下的蒸气压虽然小于平面的饱和蒸气压，但对于凹液面而言可能已经是过饱和了，此时可观察到毛细管内的蒸气凝结现象。一个典型的实例是硅胶干燥效应，由于硅胶是一种多孔性物质，具有很多毛细孔，因而具有很大的内表面，可自动吸附空气中的水蒸气，并在硅胶内部的毛细管内发生凝结现象，从而达到使空气干燥的目的。