人们在实践中发现所有弯曲的液面都存在附加压力，为了直观了解这一附加压力，可以通过下面的实验加以演示。实验装置如图1-2所示，该装置由三根充满肥皂水的H形玻璃管组成，每根管各带有一个截止阀。实验前，三个阀均处于关闭状态，首先慢慢开启阀1和阀2，分别在两垂直管下端制造大小不同的肥皂泡，设两个肥皂泡的半径分别为r1和r2，且r1＜r2，然后关闭阀1和阀2，再开启阀3使得这两个肥皂泡连通，结果会怎样呢？可以设想，如果两个泡承受的压力相同，则两者连通后将各自保持原状，否则，我们会看到其中的一个泡会越来越小，直至消失。而上述实验的结果是较小的肥皂泡在阀3开启后逐渐萎缩直至消失，这表明两个半径不同的肥皂泡所承受的压力并不相等，较小者所受压力明显大于较大者。而两个曲率半径不同的弯曲液面所承受的大气压是相等的，那么不同之处应该是与曲率半径有关的特殊压力，这里称之为附加压力，用pa表示，那么pa与r之间存在何种关系呢？我们可以设计一个可逆等温膨胀过程来加以推导。

图1-2 附加压力演示实验装置

如图1-3所示，一带有活塞且充满水的玻璃管，先以外力p1推动活塞使管端形成半径为r1的小水滴，它除受到大气压作用以外还受到附加压力pa的作用。当推动活塞的力加大到（p1＋pa）时，液滴长大，半径为r2。设此过程为恒温可逆过程，体积增加dV，面积增加dS，则有推动活塞所做的功为施加的压力pa与体积变化dV的乘积，即

图1-3 曲率半径增大的可逆过程

dW＝pa·dV （1-1）

式中，dW为外界对系统所做的功。

根据热力学第一定律可知，外界对系统所做的功全部用来增加系统的内能，由于体系恒温，所说的内能的增加应体现在表面自由能的增加。设单位面积上的自由能（比表面自由能）为Γ，则有

dW＝pa·dV＝ΓdS 　（1-2）(www.daowen.com)

根据球体的体积和面积公式可得

dV＝4πr2dr 　（1-3a）

dS＝8πrdr 　（1-3b）

将式（1-3）代入式（1-2），整理后可得

式（1-4）表明，球形液面受到的附加压力与其曲率半径r成反比，与曲率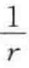成正比，附加压力的方向由曲面指向圆心，如图1-4所示。对于凹液面，附加压力为负；对于凸液面，附加压力为正；若是平液面，则附加压力为零。

图1-4 附加压力的方向与曲率半径的关系

上面所说的比表面自由能（J/m2），与表面张力（N/m）具有相同的量纲，两者在本质上是同一个参数，只是考察的角度不同：前者是单位面积上的能量，后者是单位长度上的力。后文将进一步介绍表面张力的物理意义。上述可逆实验表明表面分子具有比体相分子更大的能量，而根据能量越小越稳定的原理，总能量的最小化过程即为一自发过程，因此，当界面状况发生变化时，必然产生一系列现象，所有这些现象都与界面自由能有关，而界面自由能又与界面相的分子结构及其分子间的相互作用有关，下面将简单介绍分子间力的概念。